Phương pháp giải:

- Xác định tâm mặt cầu ngoại tiếp là điểm cách đều 4 đỉnh của tứ diện.

- Áp dụng định lí Pytago để tính bán kính \(R\) của mặt cầu.

- Diện tích mặt cầu bán kính \(R\) là \(S = 4\pi {R^2}\).

Lời giải chi tiết:

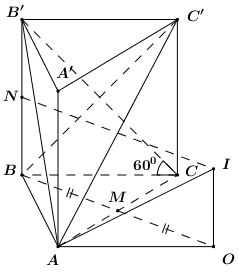
Gọi \(M\) là trung điểm của \(AC\) và \(O\) là điểm đối xứng \(B\) qua \(M\).

Ta có \(AM = MC = \frac{{a\sqrt 3 }}{2}\) và \(BM \bot AC\) (do tam giác \(ABC\) cân tại \(B\)).

Áp dụng định lí Pytago trong tam giác vuông \(ABM\) có: \(BM = \sqrt {A{B^2} - A{M^2}} \) \( = \sqrt {{a^2} - \frac{{3{a^2}}}{4}}  = \frac{a}{2}\).

\( \Rightarrow OB = 2OM = a\).

Xét tứ giác \(ABCO\) có: \(\left\{ \begin{array}{l}MA = MI\\MB = MO\\AC \bot OB\end{array} \right.\) \( \Rightarrow ABCO\) là hình thoi.

\( \Rightarrow OA = OI = AB = BC = a\).

\( \Rightarrow OA = OB = OC\) \( \Rightarrow O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\).

Gọi \(N\) là trung điểm của \(BB'\), qua \(N\) kẻ mặt phẳng vuông góc với \(BB'\) cắt đường thẳng qua \(O\) và vuông góc với \(\left( {ABC} \right)\) tại \(I\) ta có:

\(I\) thuộc đường thẳng qua \(O\) và vuông góc với \(\left( {ABC} \right)\) \( \Rightarrow IA = IB = IC\).

\(I\) thuộc mặt phẳng vuông góc với \(BB'\)  tại \(N\) \( \Rightarrow IB = IB'\).

\( \Rightarrow IA = IB = IC = IB'\) \( \Rightarrow I\) thuộc trục của \(\left( {ABB'} \right)\), chính là trục của \(\left( {ABB'A'} \right)\).

\( \Rightarrow IA = IB = IC = IB' = IA'\) \( \Rightarrow I\) thuộc trục của \(\left( {AA'C} \right)\), chính là trục của \(\left( {ACC'A'} \right)\).

\( \Rightarrow IA = IB = IC = IB' = IA' = IC'\), do đó \(I\) chính là tâm mặt cầu ngoại tiếp tứ diện \(AC'B'B\).

Ta có: \(BB' \bot \left( {ABC} \right)\)\( \Rightarrow \angle \left( {B'C;\left( {ABC} \right)} \right) = \angle \left( {B'C;BC} \right) = \angle B'CB = {60^0}\).

\( \Rightarrow BB' = BC.\tan {60^0} = a\sqrt 3 \) \( \Rightarrow OI = BN = \frac{1}{2}BB' = \frac{{a\sqrt 3 }}{2}\).

Áp dụng định lí Pytago trong tam giác vuông \(OAI\) có: \(IA = \sqrt {O{A^2} + O{I^2}} \) \( = \sqrt {{a^2} + {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}  = \frac{{a\sqrt 7 }}{2}\).

\( \Rightarrow R = \frac{{a\sqrt 7 }}{2}\) \( \Rightarrow {S_{mc}} = 4\pi {R^2} = 7\pi {a^2}\).

Chọn D.