Phương pháp giải:

Thể tích khối nón  có bán kính đáy \(R\) và chiều cao \(h:\;\;\;V = \dfrac{1}{3}\pi {R^2}h.\)

Lời giải chi tiết:

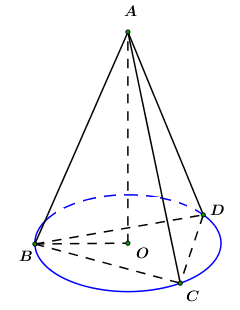
Gọi \(O\) là tâm đường tròn ngoại tiếp \(\Delta BCD.\)

Ta có bán kính đường tròn ngoại tiếp \(\Delta BCD\) là: \(R = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}.\)

Áp dụng định lý Pitago cho \(\Delta ABO\) vuông tại \(O\) ta có:

\(\begin{array}{l}OA = \sqrt {A{B^2} - O{B^2}}  = \sqrt {{a^2} - \dfrac{{{a^2}}}{3}}  = \dfrac{{a\sqrt 6 }}{3}.\\ \Rightarrow {V_{non}} = \dfrac{1}{3}\pi .O{B^2}.OA = \dfrac{1}{3}\pi .\dfrac{{{a^2}}}{3}.\dfrac{{a\sqrt 6 }}{3} = \dfrac{{\pi {a^3}\sqrt 6 }}{{27}}.\end{array}\)

Chọn  A.