Câu hỏi
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có tất cả các cạnh bằng \(a\). Gọi \(M,\,\,N\) lần lượt là trung điểm của các cạnh \(AB,\,\,B'C'\). Mặt phẳng \(\left( {A'MN} \right)\) cắt cạnh \(BC\) tại \(P\). Thể tích của khối đa diện \(MBP.A'B'N\) bằng:
- A \(\dfrac{{7\sqrt 3 {a^3}}}{{32}}.\)
- B \(\dfrac{{7\sqrt 3 {a^3}}}{{96}}.\)
- C \(\dfrac{{\sqrt 3 {a^3}}}{{24}}.\)
- D \(\dfrac{{\sqrt 3 {a^3}}}{{12}}.\)
Phương pháp giải:
Sử dụng tỉ số thể tích.
Lời giải chi tiết:
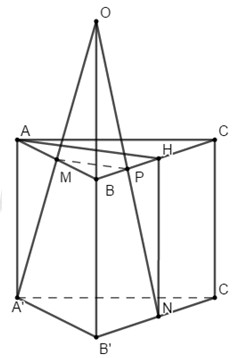
Trong \(\left( {ABB'A'} \right)\) gọi \(A'M \cap BB' = O\).
Trong mặt phẳng \(\left( {BCC'B'} \right)\) nối \(NO\) cắt \(BC\) tại \(P\).
Áp dụng định lí Ta-lét ta có:
\(\dfrac{{OM}}{{OA'}} = \dfrac{{OB}}{{OB'}} = \dfrac{{OP}}{{ON}} = \dfrac{{BM}}{{A'B'}} = \dfrac{1}{2}\).
\(\begin{array}{l} \Rightarrow \dfrac{{{V_{O.MBP}}}}{{{V_{O.A'B'N}}}} = \dfrac{{OM}}{{OA'}}.\dfrac{{OB}}{{OB'}}.\dfrac{{OP}}{{ON}} = \dfrac{1}{8}\\ \Rightarrow {V_{MBP.A'B'N}} = \dfrac{7}{8}.{V_{O.A'B'N}}\end{array}\)
Lại có
\(\begin{array}{l}{V_{OA'B'N}} = \dfrac{1}{3}.OB.{S_{A'B'N}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}OB.\dfrac{1}{2}A'B'.B'N.\sin {60^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{6}.2a.a.\dfrac{a}{2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 3 }}{{12}}\end{array}\)
Vậy \({V_{MBP.A'B'N}} = \dfrac{7}{8}.\dfrac{{{a^3}\sqrt 3 }}{{12}} = \dfrac{{7{a^3}\sqrt 3 }}{{96}}\).
Chọn B.







