Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ
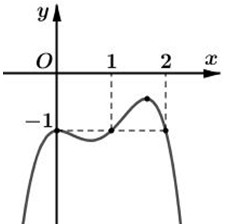
Hàm số \(g\left( x \right) = f\left( {x - 1} \right) + x + 5\) đạt cực tiểu tại điểm
- A \(x = - 1\)
- B \(x = 2\)
- C \(x = 1\)
- D \(x = 3\)
Phương pháp giải:
Xét dấu \(g'\left( x \right)\), lập BBT và kết luận.
Lời giải chi tiết:
Hàm số \(g\left( x \right) = f\left( {x - 1} \right) + x + 5\)
\( \Rightarrow g'\left( x \right) = f'\left( {x - 1} \right) + 1 = 0\) \( \Leftrightarrow f'\left( {x - 1} \right) = - 1\)\( \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 1 = 1\\x - 1 = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\\x = 3\end{array} \right.\)
Bảng biến thiên:
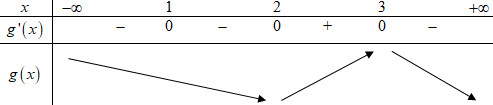
Dựa vào bảng biến thiên ta thấy hàm số \(g\left( x \right) = f\left( {x - 1} \right) + x + 5\) đạt cực tiểu khi \(x = 2\).
Chọn B.
Câu hỏi trước
