Câu hỏi
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {1;3} \right]\) và có bảng biến thiên như sau
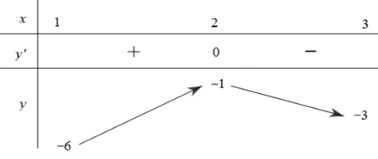
Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) để phương trình \(f\left( {x - 1} \right) = \dfrac{m}{{{x^2} - 6x + 12}}\) có hai nghiệm phân biệt trên đoạn \(\left[ {2;4} \right]\). Tổng các phần tử của \(S\) là
- A \( - 297\).
- B \( - 294\).
- C \( - 75\).
- D \( - 72\)
Phương pháp giải:
Đặt ẩn phụ rồi xét tính đơn điệu của hàm số mới, suy ra giá trị của m.
Lời giải chi tiết:
Ta có: \(f\left( {x - 1} \right) = \dfrac{m}{{{x^2} - 6x + 12}}\) \( \Leftrightarrow f\left( {x - 1} \right).\left( {{x^2} - 6x + 12} \right) = m\).
Đặt \(x - 1 = t \Rightarrow t \in \left[ {1;3} \right]\).
Khi đó ta có \(m = f\left( t \right)\left( {{t^2} - 4t + 7} \right) = g\left( t \right)\).
\(g'\left( t \right) = f'\left( t \right)\left( {{t^2} - 4t + 7} \right) + \left( {2t - 4} \right).f\left( t \right)\).
\(\begin{array}{l} + )\,\,1 \le t \le 2 \Rightarrow \left\{ \begin{array}{l}f'\left( t \right) > 0\\{t^2} - 4t + 7 > 0\\f\left( t \right) < 0\\2t - 4 \le 0\end{array} \right. \Rightarrow y' \ge 0\\ + )\,\,2 < t \le 3 \Rightarrow \left\{ \begin{array}{l}f'\left( t \right) < 0\\{t^2} - 4t + 7 > 0\\f\left( t \right) < 0\\2t - 4 > 0\end{array} \right. \Rightarrow y' < 0\end{array}\)
Ta có: \(m = f\left( t \right)\left( {{t^2} - 4t + 7} \right) = g\left( t \right)\)
\(g\left( 1 \right) = 4f\left( 1 \right) = - 24;\,\,g\left( 2 \right) = 3f\left( 2 \right) = - 3,\)\(g\left( 3 \right) = 4f\left( 3 \right) = - 12\).
Ta có bảng biến thiên hàm số \(y = g\left( x \right)\) như sau:
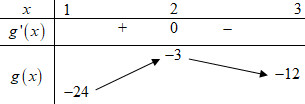
Dựa vào bảng biến thiên ta có phương trình \(f\left( {x - 1} \right) = \dfrac{m}{{{x^2} - 6x + 12}}\) có 2 nghiệm trên đoạn \(\left[ {2;4} \right]\) khi:
\( - 12 \le m < - 3;\,\,\,m \in \mathbb{Z}\)\( \Rightarrow m \in \left\{ { - 12; - 11;... - 4} \right\}\) \( \Rightarrow S = - 72.\)
Chọn D.







