Phương pháp giải:

Tìm thiết diện của hình chóp với mặt phẳng \(\left( {BMN} \right)\)

Sử dụng bài toán phụ sau để giải bài toán.

   Cho lăng trụ \(ABC.A'B'C'\) có các điểm \(M,N,P\) lần lượt nằm trên các cạnh \(AA',BB',CC'\) sao cho \(\dfrac{{AM}}{{AA'}} = x;\dfrac{{BN}}{{BB'}} = y;\dfrac{{CP}}{{CC'}} = z\)  thì tỉ số thể tích của \(\dfrac{{{V_{ABC.MNP}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{{x + y + z}}{3}\)

Lời giải chi tiết:

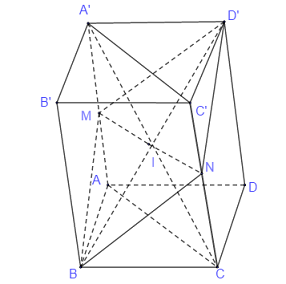
Gọi \(I\) là giao điểm của \(MN\) và \(A'C\)

Tứ giác \(A'MCN\) có \(\left\{ \begin{array}{l}A'M//CN\\A'M = CN = \dfrac{1}{2}CC'\end{array} \right.\) nên \(A'MCN\) là hình bình hành.

Do đó \(I\) là trung điểm của \(A'C\).

Mặt khác \(A'C\)  và \(BD'\) cắt nhau tại trung điểm mỗi đường nên \(I\) nằm trên \(BD'\)

Do đó thiết diện khi cắt hình hộp bởi \(mp\left( {BMN} \right)\) là tứ giác \(BMD'N\)

Khi đó, hình hộp được chia thành 2 phần, \({V_1}\) là thể tích của khối \(BMD'NACD\)

Sử dụng bài toán phụ sau:  Cho lăng trụ \(ABC.A'B'C'\) có các điểm \(M,N,P\) lần lượt nằm trên các cạnh \(AA',BB',CC'\) sao cho \(\dfrac{{AM}}{{AA'}} = x;\dfrac{{BN}}{{BB'}} = y;\dfrac{{CP}}{{CC'}} = z\)  thì tỉ số thể tích của \(\dfrac{{{V_{ABC.MNP}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{{x + y + z}}{3}\)

Ta có:

   \(\dfrac{{{V_{BMNAC}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{1}{3}\left( {\dfrac{{BB}}{{BB'}} + \dfrac{{AM}}{{AA'}} + \dfrac{{CN}}{{CC'}}} \right) = \dfrac{1}{3}\left( {0 + \dfrac{1}{2} + \dfrac{1}{2}} \right) = \dfrac{1}{3} \Rightarrow {V_{ABCMN}} = \dfrac{1}{3}{V_{ABC.A'B'C'}} = \dfrac{1}{6}{V_{ABCD.A'B'C'D'}}\)

\(\dfrac{{{V_{ACD.MND'}}}}{{{V_{ADC.A'D'C'}}}} = \dfrac{1}{3}\left( {\dfrac{{DD'}}{{DD'}} + \dfrac{{CN}}{{CC'}} + \dfrac{{AM}}{{AA'}}} \right) = \dfrac{1}{3}.\left( {1 + \dfrac{1}{2} + \dfrac{1}{2}} \right) = \dfrac{2}{3} \Rightarrow {V_{MND'.ACD}} = \dfrac{1}{3}{V_{ABCD.A'B'C'D'}}\)

Do đó,  

               \(\begin{array}{l}{V_1} = {V_{BMD'NADC}} = {V_{ACD.MND'}} + {V_{BMNAC}} = \left( {\dfrac{1}{3} + \dfrac{1}{6}} \right){V_{ABC.A'B'C'}} = \dfrac{1}{2}V\\ \Rightarrow {V_2} = \dfrac{1}{2}V \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = 1\end{array}\)

Chọn D.