Phương pháp giải:

Lăng trụ đều là lăng trụ đứng có đáy là đa giác đều

Tìm góc tạo bởi \(SC\) và mặt phẳng \(\left( {ABB'A'} \right)\) để tính độ dài cạnh bên của lăng trụ

Thể tích của lăng trụ đều \(ABC.A'B'C'\) được tính bởi công thức    \(V = AA'.{S_{ABC}}\)

Lời giải chi tiết:

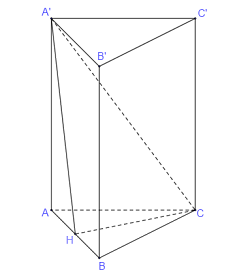
Gọi \(H\) là trung điểm của \(AB\). Do tam giác \(ABC\) là tam giác đều nên \(CH \bot AB\)

\(ABC.A'B'C'\) là lăng trụ đều nên cạnh bên vuông góc với đáy hay \(AA' \bot \left( {ABC} \right) \Leftrightarrow AA' \bot CH\)

Suy ra  \(CH \bot \left( {ABB'A'} \right)\)

Do đó góc tạo bởi \(A'C\) và mặt phẳng \(\left( {ABB'A'} \right)\) là góc giữa \(A'C\) và \(A'H\)  hay \(\widehat {HA'C} = 30^\circ \)

\(CH\) là đường trung bình trong tam giác đều \(ABC\) nên \(CH = \dfrac{{\sqrt 3 }}{2}.AB = \dfrac{{\sqrt 3 }}{2}.\sqrt 2 a = \dfrac{{\sqrt 6 }}{2}a\)

Tam giác \(A'HC\) vuông tại \(H\)  nên \(\tan HA'C = \dfrac{{HC}}{{A'H}} \Rightarrow A'H = \dfrac{{3\sqrt 2 }}{2}a\)

Suy ra  \(AA{'^2} = \sqrt {A'{H^2} - A{H^2}}  = \sqrt {{{\left( {\dfrac{{3\sqrt 2 }}{2}a} \right)}^2} - {{\left( {\dfrac{{\sqrt 2 }}{2}a} \right)}^2}}  = 2a\)

Vậy thể tích của khối lăng trụ \(ABC.A'B'C'\)  là \(V = AA'.{S_{ABC}} = AA'.\dfrac{1}{2}AB.CH = \dfrac{1}{2}.2a.\sqrt 2 a.\dfrac{{\sqrt 6 }}{2}a = \sqrt 3 {a^3}\)

Chọn D