Câu hỏi
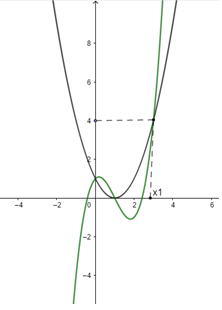
Cho hàm số \(y = f\left( x \right)\) có đồ thị của hàm số \(y = f'\left( x \right)\) như hình vẽ. Hàm số \(g\left( x \right) = f\left( x \right) - \frac{{{x^2}}}{3} + {x^2} - x + 2\) đạt cực đại tại điểm nào ?
- A \(x=-1\)
- B \(x=0\)
- C \(x=1\)
- D \(x=2\)
Phương pháp giải:
Tìm đạo hàm của hàm số \(g'\left( x \right)\).
Sử dụng đồ thị để tìm nghiệm của phương trình \(g'\left( x \right)\)=0.
Lập bảng biến thiên của hàm số \(g\left( x \right)\) để tìm cực đại.
Lời giải chi tiết:
Ta có \(g\left( x \right) = f\left( x \right) - \frac{{{x^2}}}{3} + {x^2} - x + 2\)
\(\begin{array}{l} \Rightarrow g'\left( x \right) = f'\left( x \right) - {x^2} + 2x - 1\\g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = {x^2} - 2x + 1 = {\left( {x - 1} \right)^2}\end{array}\)
Đồ thị hàm số \(y = {\left( {x - 1} \right)^2}\) có dạng parabol, đỉnh là \(I\left( {1;0} \right)\) và đi qua \(A\left( {0;1} \right);B\left( {2;1} \right)\).
Dựa vào đồ thị ta thấy đồ thị hàm số \(y = f\left( x \right);y = {\left( {x - 1} \right)^2}\) cắt nhau tại 3 điểm có hoảnh độ là \(0;1;{x_1}\left( {{x_1} > 1} \right)\)
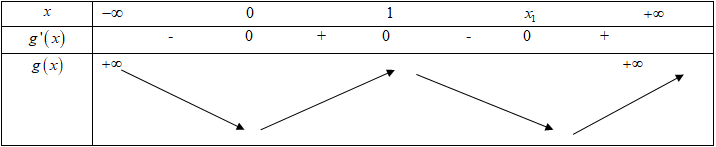
Bảng biến thiên:
Dựa vào bảng biến thiên ta có: hàm số \(g\left( x \right)\) đạt giá trị cực đại tại \(x = 1.\)
Chọn C.