Câu hỏi
Cho một hình nón đỉnh \(I\) có đường tròn đáy là đường tròn đường kính \(AB = 6cm\) và đường cao bằng \(3\sqrt 3 cm.\) Gọi \(\left( S \right)\) là mặt cầu chứa đỉnh \(I\) và đường tròn đáy của hình nón. Bán kính của mặt cầu \(\left( S \right)\) bằng
- A \(3\sqrt 2 \left( {cm} \right).\)
- B \(2\sqrt 3 \left( {cm} \right).\)
- C \(3\sqrt 3 \left( {cm} \right).\)
- D \(\sqrt 3 \left( {cm} \right).\)
Phương pháp giải:
- Xác định tâm mặt cầu.
- Chứng minh tâm mặt cầu trùng với tâm đường tròn ngoại tiếp tam giác IAB.
- Chứng minh tam giác IAB đều.
- Sử dụng công thức tính nhanh bán kính đường tròn ngoại tiếp tam giác đều cạnh a là \(R = \dfrac{{a\sqrt 3 }}{2}\).
Lời giải chi tiết:
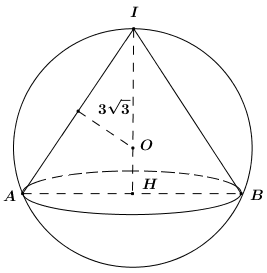
Mặt cầu chứa đỉnh I chứa đường tròn đường kính AB nên mặt cầu đi qua A, B.
Do đó bán kính mặt cầu chính là bán kính đường tròn ngoại tiếp tam giác IBC.
Tam giác IAB có IA = IB = l, suy ra tam giác IAB cân tại I.
Gọi H là trung điểm của AB \( \Rightarrow SH \bot AB\) và AH = 3cm, \(IH = 3\sqrt 3 cm\).
Áp dụng định lí Pytago trong tam giác vuông IAH ta có:
\(IA = \sqrt {I{H^2} + A{H^2}} = \sqrt {27 + 9} = 6\,\,\left( {cm} \right) = IB\).
\( \Rightarrow \Delta IAB\) đều cạnh 6cm.
Vậy bán kính đường tròn ngoại tiếp tam giác IAB là \(R = \dfrac{{6\sqrt 3 }}{2} = 3\sqrt 3 \,\,\left( {cm} \right)\).
Đáp án C.







