Câu hỏi
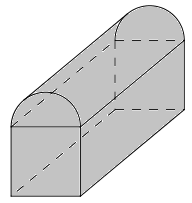
Một hộp nữ trang được tạo thành từ một hình lập phương cạnh \(6cm\) và một nửa hình trụ có đường kính đáy bằng \(6cm\) (hình bên). Thể tích của hộp nữ trang này bằng:
- A \(216 + 108\pi \left( {c{m^3}} \right).\)
- B \(216 + 54\pi \left( {c{m^3}} \right).\)
- C \(216 + 27\pi \left( {c{m^3}} \right).\)
- D \(36 + 27\pi \left( {c{m^3}} \right).\)
Phương pháp giải:
Thể tích một nữ trang bằng tổng thể tích khối lập phương và nửa khối trụ.
Lời giải chi tiết:
+ Thể tích khối lập phương cạnh 6 cm là \({V_1} = {6^3} = 216\,\,\left( {c{m^3}} \right)\).
+ Thể tích nửa khối trụ bán kính đáy r = 3cm, đường cao h = 6 cm là:
\({V_2} = \dfrac{1}{2}.\left( {\pi {r^2}h} \right) = \dfrac{1}{2}\pi {.3^2}.6 = 27\pi \,\,\left( {c{m^3}} \right)\).
Vậy thể tích một nữ trang là \(V = {V_1} + {V_2} = 216 + 27\pi \,\,\left( {c{m^3}} \right)\).
Đáp án C.
Câu hỏi trước
