Câu hỏi
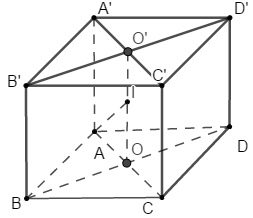
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên \(A'A = a\sqrt 2 .\) Mặt cầu đi qua tất cả các đỉnh của khối họp chữ nhật có bán kính bằng :
- A \(a\)
- B \(a\sqrt 3 .\)
- C \(\frac{{3a}}{2}.\)
- D \(a\sqrt 2 .\)
Phương pháp giải:
- Tìm tâm của mặt cầu ngoại tiếp hình lập phương.
- Áp dụng định lí Pytago để tính bán kính của mặt cầu.
Lời giải chi tiết:
Gọi \(O,\,\,O'\) lần lượt là tâm của hình vuông \(ABCD,\,\,A'B'C'D'\).
Gọi \(I\) là trung điểm của \(OO'\). Suy ra \(I\) cách đều 8 đỉnh của hình lập phương nên \(I\) là tâm mặt cầu cần tìm.
Hình vuông \(ABCD\) có cạnh bằng \(a\)\( \Rightarrow AO = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}.\)
Mặt khác: \(OI = \frac{{A'A}}{2} = \frac{{a\sqrt 2 }}{2}.\)
Áp dụng định lí Pytago trong tam giác vuông \(AOI\) có:
\(AI = \sqrt {A{O^2} + O{I^2}} = \sqrt {{{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = a\)
Chọn A.