Câu hỏi
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?
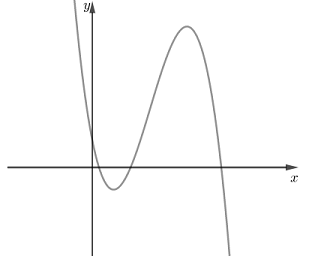
- A \(a < 0,b > 0,c > 0,d > 0\)
- B \(a < 0,b < 0,c < 0,d > 0\)
- C \(a < 0,b > 0,c < 0,d > 0\)
- D \(a < 0,b < 0,c > 0,d > 0\)
Phương pháp giải:
- Từ đồ thị của hàm số, xác định điểm cắt của đồ thị với trục tung, giới hạn của hàm số ở \( \pm \infty \), dấu của các điểm cực trị.
- Từ đó suy ra dấu của \(a,b,c,d\).
Lời giải chi tiết:
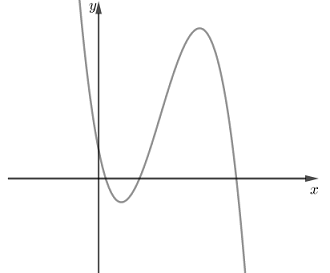
Từ đồ thị hàm số đã cho ta thấy :
Đồ thị hàm số cắt trục tung tại một điểm có tung độ lớn hơn 0 nên \(d > 0\)
\(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \) nên \(a < 0\)
Hàm số có 2 điểm cực trị \({x_1};{x_2}\) thỏa mãn \({x_1} > 0;{x_2} > 0\) nên ta có :
\({x_1};{x_2}\) là 2 nghiệm dương phân biệt của phương trình
\(y' = 0 \Leftrightarrow 3a{x^2} + 2bx + c = 0\) nên:
\(\left\{ \begin{array}{l}{x_1} + {x_2} > 0\\{x_1}.{x_2} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{ - 2b}}{{3a}} > 0\\\dfrac{c}{{3a}} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{b}{a} < 0\\\dfrac{c}{a} > 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a < 0\\b > 0\\c < 0\end{array} \right.\)
Vậy \(a < 0,\,\,b > 0,\,\,c < 0,\,\,d > 0.\)
Chọn C.







