Phương pháp giải:

Xác định điểm cách đều bốn đỉnh của hình chóp từ đó tính bánh kính mặt cầu ngoại tiếp hình chóp

Lời giải chi tiết:

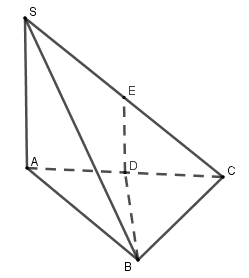
Gọi \(D\) và \(E\) lần lượt là trung điểm của \(AC,SC\).

Ta có \(DE//SA \Rightarrow DE \bot \left( {ABC} \right)\) mà \(D\) là tâm đường tròn ngoại tiếp tam giác \(ABC\) nên \(ED\) là trục đường trong ngoại tiếp đáy. Do đó: \(EA = EB = EC\)

Lại có tam giác \(SAC\) vuông tại \(A\) có \(E\) là trung điểm cạnh huyền nên \(EA = ES = EC = \dfrac{{SC}}{2}\)

Suy ra \(EA = ES = EC = EB = \dfrac{{SC}}{2}\) hay \(E\) là tâm mặt cầu ngoại tiếp chóp \(S.ABC\) và bán kính mặt cầu là \(\dfrac{{SC}}{2}\)

Xét tam giác \(ABC\) vuông tại \(B\) ta có: \(AC = \sqrt {B{C^2} + B{A^2}}  = a\sqrt 2 \)

Xét tam giác \(SAC\) vuông tại \(A\) ta có: \(SC = \sqrt {S{A^2} + A{C^2}}  = \sqrt {4{a^2} + 2{a^2}}  = a\sqrt 6 \)

Bán kính mặt cầu cần tìm là: \(R = \dfrac{{SC}}{2} = \dfrac{{a\sqrt 6 }}{2}.\)

Chọn D.