Phương pháp giải:

- Sử dụng đạo hàm hợp tính đạo hàm hàm số \(g\left( x \right)\).

- Giải phương trình \(g'\left( x \right) = 0\) và kết luận số cực trị của hàm số.

Lời giải chi tiết:

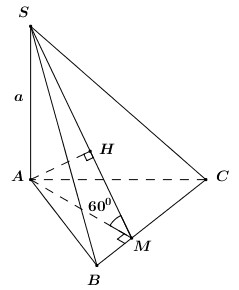
Trong \(\left( {ABC} \right)\) kẻ \(AM \bot BC\,\,\left( {M \in BC} \right)\) ta có:

\(\left\{ \begin{array}{l}BC \bot AM\\BC \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right) \Rightarrow BC \bot SM\).

Ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SM \bot BC\\\left( {ABC} \right) \supset AM \bot BC\end{array} \right.\).

\( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle \left( {SM;AM} \right) = \angle SMA = {60^0}\).

Vì \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AM \Rightarrow \Delta SAM\) vuông tại \(A\).

Mà \(\widehat {SMA} = {60^0} \Rightarrow \widehat {ASM} = {30^0}\).

Trong \(\left( {SAM} \right)\) kẻ \(AH \bot SM\), xét tam giác vuông \(SAH\) có:  \(AH = SA.\sin {30^0} = \dfrac{a}{2}\).

Ta có: \(\left\{ \begin{array}{l}AH \bot SM\\AH \bot BC\,\,\left( {BC \bot \left( {SAM} \right)} \right)\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right)\).

\( \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AH = \dfrac{a}{2} = d\).

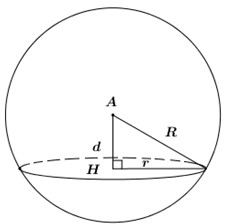
Giả sử mặt cầu tâm \(A\), bán kính \(R = \dfrac{{a\sqrt 3 }}{2}\) cắt \(\left( {SBC} \right)\) theo giao tuyến là một đường tròn có bán kính \(r\).

Áp dụng định lí Pytago ta có: \(r = \sqrt {{R^2} - {d^2}}  = \sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} - {{\left( {\dfrac{a}{2}} \right)}^2}}  = \dfrac{{a\sqrt 2 }}{2}\).

Chọn A.