Câu hỏi
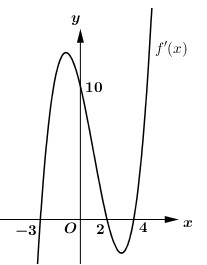
Cho hàm số \(f\left( x \right)\), hàm số \(y = f'\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số \(g\left( x \right) = f\left( {{x^2} + x} \right)\) là:
- A 5
- B 2
- C 4
- D 3
Phương pháp giải:
- Sử dụng đạo hàm hợp tính đạo hàm hàm số \(g\left( x \right)\).
- Giải phương trình \(g'\left( x \right) = 0\) và kết luận số cực trị của hàm số.
Lời giải chi tiết:
Từ đồ thị hàm số ta thấy \(f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 4\\x = - 3\end{array} \right.\).
Ta có: \(g\left( x \right) = f\left( {{x^2} + x} \right) \Rightarrow g'\left( x \right) = \left( {2x + 1} \right)f'\left( {{x^2} + x} \right)\).
Khi đó \(g'\left( x \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{1}{2}\\f'\left( {{x^2} + x} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{1}{2}\\{x^2} + x = 2\\{x^2} + x = 4\\{x^2} + x = - 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{1}{2}\\x = 1\\x = - 2\\x = \dfrac{{ - 1 + \sqrt {17} }}{2}\\x = \dfrac{{ - 1 - \sqrt {17} }}{2}\end{array} \right.\)
Mỗi nghiệm trên đều là nghiệm bội lẻ của phương trình \(g'\left( x \right) = 0\).
Vậy số điểm cực trị của hàm số \(g\left( x \right) = f\left( {{x^2} + x} \right)\) chính là số nghiệm của phương trình \(g'\left( x \right) = 0\) và bằng 5.
Chọn A.







