Phương pháp giải:

Mặt cầu ngoại tiếp khối trụ có tâm là trung điểm đoạn nối tâm hai đáy của khối trụ

Thể tích của khối trụ được tính bằng công thức: \(V = \pi {r^2}h\)  (\(r:\) bán kính đáy, \(h:\) chiều cao của khối trụ)

Tìm mối liên hệ giữa \(r,h,R\) để tìm thể tích lớn nhất của khối trụ

Lời giải chi tiết:

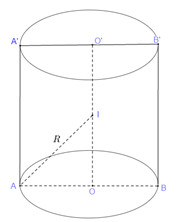
Gọi \(r\) là bán kính đáy,   \(h\) là chiều cao của khối trụ đã cho

Gọi \(AB\) là đường kính của mặt đáy tâm \(O,\) \(A'B'\) là đường kính của mặt đáy tâm \(O'\) của hình trụ sao cho \(AA'\) và \(BB'\) vuông góc với mặt phẳng đáy

Gọi \(I\) là trung điểm của \(OO'\) khi đó \(I\) là tâm mặt cầu ngoại tiếp khối trụ trên và \(IA = IB = R\)

Ta có: \(OO' \bot AB \Rightarrow I{O^2} + A{O^2} = I{A^2} \Leftrightarrow \dfrac{{{h^2}}}{4} + {r^2} = {R^2}\)

Thể tích của khối trụ trên là \(V = \pi {r^2}h\) .

Áp dụng bất đẳng thức AM – GM ta có:

\(\begin{array}{l}{R^2} = {r^2} + \dfrac{{{h^2}}}{4} = \dfrac{{{r^2}}}{2} + \dfrac{{{r^2}}}{2} + \dfrac{{{h^2}}}{4} \ge 3\sqrt[3]{{\dfrac{{{r^4}{h^2}}}{{16}}}}\\ \Rightarrow \dfrac{{{r^4}{h^2}}}{{16}} \le {\left( {\dfrac{{{R^2}}}{3}} \right)^3} \Leftrightarrow {r^2}h \le 4\sqrt {\dfrac{{{R^6}}}{{27}}}  = \dfrac{{4{R^3}}}{{3\sqrt 3 }}\end{array}\)

\( \Rightarrow V = \pi {r^2}h \le \dfrac{{4\pi {R^3}}}{{3\sqrt 3 }}\)

Dấu ‘=’ xảy ra khi và chỉ khi \(\dfrac{{{r^2}}}{2} = \dfrac{{{h^2}}}{4} = \dfrac{{{R^2}}}{3} \Rightarrow \left\{ \begin{array}{l}r = \dfrac{{\sqrt 6 }}{3}R\\h = \dfrac{{2\sqrt 3 }}{3}R\end{array} \right.\)

Vậy để khối trụ có thể tích lớn nhất thì chiều cao của khối trụ bằng \(\dfrac{{2R\sqrt 3 }}{3}\)

Chọn B.