Câu hỏi
Cho lăng trụ \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(a\). HÌnh chiếu của điểm \(A'\) lên mặt phẳng \(\left( {ABC} \right)\) là tâm \(O\) của đường tròn ngoại tiếp tam giác \(ABC\). Góc tạo bởi \(AA'\) và \(\left( {ABC} \right)\) bằng \(60^\circ \). Tính thể tích \(V\) của khối đa diện \(A'.B'C'CB\). (tham khảo hình vẽ)
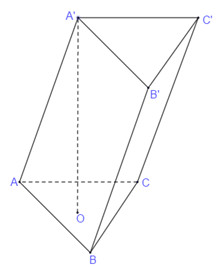
- A \(V = \dfrac{{{a^3}\sqrt 3 }}{6}\)
- B \(V = \dfrac{{{a^3}\sqrt 3 }}{{12}}\)
- C \(V = \dfrac{{{a^3}\sqrt 3 }}{{24}}\)
- D \(V = \dfrac{{{a^3}\sqrt 3 }}{4}\)
Phương pháp giải:
- Tìm góc tạo bởi \(AA'\) và \(\left( {ABC} \right)\).
- Tính đường cao \(A'O\) của lăng trụ.
- Thể tích của lăng trụ được tính bởi công thức \({V_{ABC.A'B'C'}} = A'O.{S_{\Delta ABC}}\).
- Tính tỉ số \(\dfrac{{{V_{A'.B'C'CB}}}}{{{V_{ABC.A'B'C'}}}}\) để suy ra \({V_{A'.B'C'CB}}\).
Lời giải chi tiết:
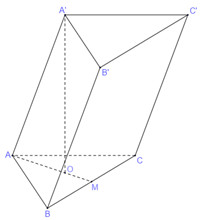
Do \(O\) là hình chiếu vuông góc của \(A'\) lên mặt phẳng \(\left( {ABC} \right)\) nên góc tạo bởi \(AA'\) và \(\left( {ABC} \right)\) là góc giữa \(AA'\) và \(AO\), do đó \(\angle A'AO = {60^0}\).
Gọi \(M\) là trung điểm \(BC\). Do \(ABC\) là tam giác đều nên \(A,\,\,O,\,\,M\) thẳng hàng.
Tam giác \(ABC\) là tam giác đều cạnh \(a\) nên \(AM = \dfrac{{\sqrt 3 }}{2}AB = \dfrac{{\sqrt 3 }}{2}a\).
Suy ra \(AO = \dfrac{2}{3}AM = \dfrac{{\sqrt 3 }}{3}a\).
Xét tam giác vuông \(A'AO\) có: \(\tan A'AO = \dfrac{{A'O}}{{AO}} \Leftrightarrow \tan {60^0} = \dfrac{{A'O}}{{\dfrac{{\sqrt 3 }}{3}a}} \Rightarrow A'O = a.\)
Thể tích của khối lăng trụ \(ABC.A'B'C'\) là \({V_{ABC.A'B'C'}} = A'O.{S_{ABC}} = a.\dfrac{{\sqrt 3 }}{4}{a^2} = \dfrac{{\sqrt 3 }}{4}{a^3}\)
Ta có :
\(\begin{array}{l}{V_{A'.ABC}} = \dfrac{1}{3}A'O.{S_{ABC}} = \dfrac{1}{3}{V_{ABC.A'B'C'}}\\ \Rightarrow {V_{A'.B'C'CB}} = {V_{ABC.A'B'C'}} - {V_{A'.ABC}} = \dfrac{2}{3}{V_{ABC.A'B'C'}}\end{array}\)
Suy ra thể tích \(V\) của khối đa diện \(A'.B'C'CB\) là \(V = \dfrac{2}{3}{V_{ABC.A'B'C'}} = \dfrac{2}{3}.\dfrac{{\sqrt 3 }}{4}.{a^3} = \dfrac{{\sqrt 3 }}{6}{a^3}\).
Chọn A.







