Phương pháp giải:

Thiết diện qua trục của hình nón là một tam giác cân có cạnh đáy là đường kính đáy, hai cạnh bên là đường sinh của hình nón.

Diện tích xung quanh của hình nón bán kính đáy \(r\), đường sinh \(l\) được tính bởi công thức \({S_{xq}} = \pi rl\).

Lời giải chi tiết:

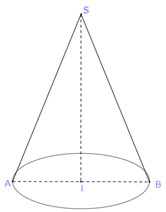
Gọi \(r\) là bán kính đáy, \(l\) là độ dài đường sinh của hình nón.

Thiết diện qua trục của hình nón là một tam giác đều nên \(l = 2r\).

Do đó diện tích thiết diện là \(S = \dfrac{{{l^2}\sqrt 3 }}{4}\).

Theo bài ra ta có: \(\dfrac{{\sqrt 3 }}{4}.{l^2} = {a^3}\sqrt 3  \Rightarrow l = 2a \Rightarrow r = a.\) 

Diện tích xung qunh của hình nón là: \({S_{xq}} = \pi rl = \pi .a.2a = 2\pi {a^2}\).

Chọn C.