Môn Lý - Lớp 12
Môn Lý - Lớp 12
 50 bài tập Tổng hợp hai dao động điều hòa cùng phương, cùng tần số - Phương pháp giản đồ Frenen mức độ vận dụng cao
50 bài tập Tổng hợp hai dao động điều hòa cùng phương, cùng tần số - Phương pháp giản đồ Frenen mức độ vận dụng cao
Câu hỏi
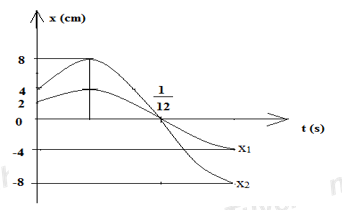
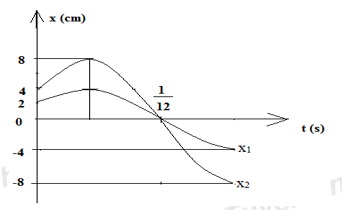
Hai dao động điều hòa cùng phương, cùng tần số, có đồ thị tọa độ theo thời gian như hình vẽ. Một chất điểm thực hiện đồng thời hai dao động trên. Vận tốc của chất điểm khi qua li độ \(x = 6{\sqrt 3 _{}}cm\) có độ lớn là:
- A 60π cm/s
- B 120π cm/s
- C 40π cm/s
- D 140π cm/s
Phương pháp giải:
Từ đồ thị ta viết phương trình của hai phương trình x1 và x2 sau đó tổng hợp x = x1+ x2
Sau đó áp dụng công thức độc lập với thời gian:
\({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}\)
Lời giải chi tiết:
+ Dao động của vật 1 có biên độ A = 4 cm.
Tại thời điểm ban đầu t0 = 0 thì x10 = 2cm và vật đang chuyển động về biên dương, nên pha ban đầu
\({\varphi _1} = - \frac{\pi }{3}rad\)
Vì vậy phương trình dao động có dạng:
\({x_1} = 4.\cos \left( {\omega t - \frac{\pi }{3}} \right)(cm)\)
Đến thời điểm \(t = \frac{1}{{12}}s\) thì lần đầu tiên x1 = 0, ta có:
\(0 = 4.cos\left( {\omega .\frac{1}{{12}} - \frac{\pi }{3}} \right) \Leftrightarrow \omega .\frac{1}{{12}} - \frac{\pi }{3} = \frac{\pi }{2}\)
\( \Leftrightarrow \omega \frac{1}{{12}} = \frac{{5\pi }}{6} \Leftrightarrow \omega = 10\pi (rad/s)\)
Vậy ta có phương trình dao động của vật 1 là
\({x_1} = 4.\cos \left( {10\pi t - \frac{\pi }{3}} \right)\left( {cm} \right)\)
+ Dao động của vật 2 có biên độ A = 8cm.
Tại thời điểm ban đầu t0 = 0 thì x20= 4cm và vật đang chuyển động về biên dương, nên pha ban đầu \({\varphi _1} = - \frac{\pi }{3}rad\)
Vì vậy phương trình dao động có dạng:
\({x_2} = 8.\cos \left( {\omega t - \frac{\pi }{3}} \right)(cm)\)
Đến thời điểm \(t = \frac{1}{{12}}s\) thì lần đầu tiên x2 = 0, ta có:
\(0 = 8.cos\left( {\omega .\frac{1}{{12}} - \frac{\pi }{3}} \right) \Leftrightarrow \omega .\frac{1}{{12}} - \frac{\pi }{3} = \frac{\pi }{2}\)
\( \Leftrightarrow \omega \frac{1}{{12}} = \frac{{5\pi }}{6} \Leftrightarrow \omega = 10\pi (rad/s)\)
Vậy ta có phương trình dao động của vật 2 là:
\({x_2} = 8.\cos \left( {10\pi t - \frac{\pi }{3}} \right)\left( {cm} \right)\)
Phương trình dao động tổng hợp là:
\(x = {x_1} + {x_2}\)
\(x = 4.\cos \left( {10\pi t - \frac{\pi }{3}} \right) + 8.\cos \left( {10\pi t - \frac{\pi }{3}} \right)\)
\(x = 12.\cos \left( {10\pi t - \frac{\pi }{3}} \right)\)
Khi \(x = 6{\sqrt 3 _{}}cm\) áp dụng phương trình độc lập với thời gian ta có:
\({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Leftrightarrow {\left( {6\sqrt 3 } \right)^2} + \frac{{{v^2}}}{{{{(10\pi )}^2}}} = {12^2} \Rightarrow v = 60\pi \left( {cm/s} \right)\)
Chọn A.