Phương pháp giải:

a) Lập bảng giá trị của hai hàm số và vẽ chúng trên cùng 1 mặt phẳng tọa độ

b) Xét phương trình hoành độ giao điểm của hai đồ thị để tìm \(x,\)  thay giá trị \(x\)  vừa tìm được vào 1 trong hai phương trình để tìm \(y.\)

c) 3 đường thẳng đồng quy khi và chỉ khi đường thẳng thứ ba đi qua giao điểm của hai đường thẳng còn lại.

Lời giải chi tiết:

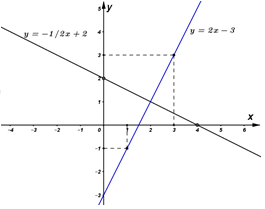
a) Vẽ đồ thị hàm số sau trên cùng một mặt phẳng tọa độ:

\(\left( {{d_1}} \right):y = 2x - 3\) và \(\left( {{d_2}} \right):y =  - \frac{1}{2}x + 2\)

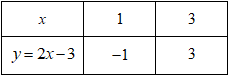
+) Vẽ đồ thị hàm số \(\left( {{d_1}} \right):y = 2x - 3\):

Bảng giá trị:

Vậy đồ thị hàm số \(\left( {{d_1}} \right)\) là đường thẳng đi qua hai điểm \(\left( {1; - 1} \right);\left( {3;3} \right)\) +) Vẽ đồ thị hàm số \(\left( {{d_2}} \right):y =  - \frac{1}{2}x + 2\)

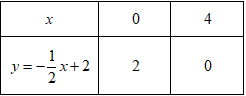
Bảng giá trị:

Vậy đồ thị hàm số \(\left( {{d_2}} \right)\) là đường thẳng đi qua hai điểm \(\left( {0;2} \right);\left( {4;0} 

b) Tìm tọa độ giao điểm \(A\)  của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) (bằng phép tính).

Xét phương trình hoành độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\):

\(2x - 3 =  - \frac{1}{2}x + 2 \Leftrightarrow 2x + \frac{1}{2}x = 2 + 3 \Leftrightarrow \frac{5}{2}x = 5 \Leftrightarrow x = 2\)

Thay \(x = 2\) vào hàm số \(y = 2x - 3\) ta được \(y = 2.2 - 3 = 1.\)

Vậy tọa độ giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \(A\left( {2;1} \right)\).

c) Tìm \(m\)  để ba đường thẳng \(\left( {{d_1}} \right)\), \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right):y = 3x - 2m - 3\) đồng quy.

Ba đường thẳng \(\left( {{d_1}} \right)\) , \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right):y = 3x - 2m - 3\) đồng quy  \( \Rightarrow \left( {{d_3}} \right)\) đi qua giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\)\( \Rightarrow A \in \left( {{d_3}} \right)\)

Thay tọa độ điểm \(A\)  vào hàm số \(\left( {{d_3}} \right):\,\,y = 3x - 2m - 3\) ta được:

\(1 = 3.2 - 2m - 3\)\( \Rightarrow 2m = 6 - 3 - 1 \Rightarrow m = 1\)

Vậy \(m = 1\) thì ba đường thẳng  \(\left( {{d_1}} \right)\) , \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right):y = 3x - 2m - 3\) đồng quy.

Chọn A.