Phương pháp giải:

Hàm số \(y = ax + b\,\,\,\left( {a \ne 0} \right)\)đồng biến khi \(a > 0\) và nghịch biến khi \(a < 0\).

Lời giải chi tiết:

Hàm số \(y = mx - 2\) đồng biến\( \Leftrightarrow m > 0\)

Vậy \(m > 0.\)

Chọn A.

Phương pháp giải:

Một điểm thuộc 1 đường thẳng khi tọa độ điểm đó thỏa mãn phương trình đường thẳng.

Vẽ đồ thị hàm số bằng cách lập bảng giá trị.

Lời giải chi tiết:

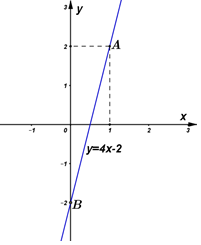
Đường thẳng \(\left( {{d_m}} \right)\) đi qua điểm \(A\left( {1;2} \right)\) nên ta thay tọa độ điểm \(A\)  vào phương trình đường thẳng  \(\left( {{d_m}} \right)\)ta được:  \(2 = m.1 - 2 \Rightarrow m = 4\)

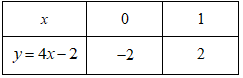
Khi \(m = 4\) đường thẳng có phương trình \(y = 4x - 2\), ta có bảng giá trị:

Vậy đồ thị hàm số khi \(m = 4\) chính là đường thẳng đi qua hai điểm\(B\left( {0; - 2} \right)\) và \(A\left( {1;2} \right)\)

Phương pháp giải:

Tìm giao điểm của đường thẳng và 2 trục tọa độ, tam giác tạo thành là tam giác vuông.

Lời giải chi tiết:

Điều kiện: \(m \ne 0.\)

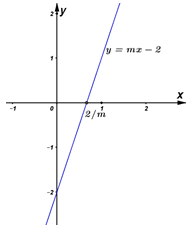
+) Với \(y = 0 \Rightarrow mx - 2 = 0 \Rightarrow mx = 2 \Rightarrow x = \frac{2}{m}\)

\( \Rightarrow \left( {{d_m}} \right):y = mx - 2\) với  cắt \(Ox\) tại điểm \(A\left( {\frac{2}{m};\,\,0} \right).\)

+) Với \(x = 0 \Rightarrow y =  - 2 \Rightarrow B\left( {0;\,\, - 2} \right)\) là giao của \(\left( {{d_m}} \right)\) và \(Oy.\)

Khi đó diện tích của tam giác sẽ là:

\(\begin{array}{l}{S_{OAB}} = \frac{1}{2}OA.OB = \frac{1}{2}.\left| {\frac{2}{m}} \right|.\left| { - 2} \right| = \frac{2}{{\left| m \right|}} = 1\\ \Leftrightarrow \left| m \right| = 2 \Leftrightarrow \left[ \begin{array}{l}m = 2\\m =  - 2\end{array} \right..\end{array}\)

Vậy \(m = 2\)hoặc \(m =  - 2\)thì đường thẳng \(\left( {{d_m}} \right)\) cắt hai trục tọa độ tạo thành tam giác có diện tích bằng 1.

Chọn D.