Phương pháp giải:

Để tính bán kính đường tròn đáy khi đã có độ dài dây cung, ta nên đi tìm khoảng cách từ tâm đến dây cung.

Lời giải chi tiết:

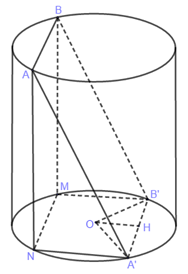
Vẽ một mặt phẳng đi qua \(AB\) và vuông góc với mặt phẳng đáy, cắt mặt đáy còn lại theo dây cung \(MN.\)

Gọi \(O\) là tâm đường tròn đáy chứa dây cung \(A'B'\) , \(H\) là trung điểm \(A'B'\)

Theo giả thiết \(ABB'A'\)là hình chữ nhật nên \(AA' \bot A'B'\)    (1)

\(AM\) vuông góc với 2 đáy nên \(AM \bot A'B'\)                        (2)

Từ (1) và (2) suy ra \(A'B' \bot \left( {AMA'} \right) \Rightarrow A'B' \bot MA'\) . Do đó \(MNB'A'\) là hình chữ nhật.

Diện tích hình chữ nhật \(ABB'A'\) bằng \(60c{m^2}\) nên

\(AA'.A'B' = 60 \Rightarrow AA' = 10\,\,\left( {cm} \right).\)

Chiều cao của khối trụ bằng \(6\sqrt 2 \left( {cm} \right) \Rightarrow AM = 6\sqrt 2 \,\,\left( {cm} \right)\).

Ta có: \(MB' = \sqrt {BB{'^2} - B{M^2}}  = \sqrt {{{10}^2} - {{\left( {6\sqrt 2 } \right)}^2}}  = 2\sqrt 7 \,\,\left( {cm} \right).\)

Do \(MNB'A'\) là hình chữ nhật nên:

\(R = \dfrac{1}{2}MA' = \dfrac{1}{2}\sqrt {MB{'^2} + A'B{'^2}}  = \dfrac{1}{2}\sqrt {{{\left( {2\sqrt 7 } \right)}^2} + {6^2}}  = 4\,\,\left( {cm} \right).\)

Vậy bán kính của đường tròn đáy bằng \(4cm\).

Chọn C.