Phương pháp giải:

- Tính tỉ số thể tích giữa khối chóp \(S.ADE\) và khối chóp \(S.ABC\)

- Tính thể tích lớn nhất của khối chóp \(S.ABC\) để suy ra thể tích lớn nhất của khối chóp \(S.ABC\)

Lời giải chi tiết:

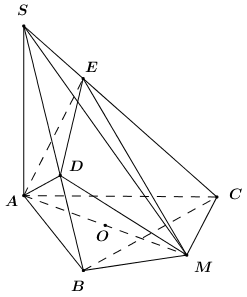
Ta có: \(\left\{ \begin{array}{l}SB = \sqrt {S{A^2} + A{B^2}}  = \sqrt {10} \\SC = \sqrt {S{A^2} + A{C^2}}  = \sqrt {13} \end{array} \right.\).

Gọi \(AM\) là đường kính lớn của mặt cầu ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}MB \bot AB\\MB \bot SA\end{array} \right. \Rightarrow MB \bot \left( {SAB} \right) \Rightarrow MB \bot AD\\AD \bot DM \Rightarrow AD \bot \left( {SBM} \right) \Rightarrow AD \bot SB\end{array}\)

Áp dụng hệ thức lượng trong tam giác vuông ta có:

\(S{A^2} = SD.SB \Leftrightarrow \dfrac{{SD}}{{SB}} = \dfrac{{S{A^2}}}{{S{B^2}}} = \dfrac{9}{{10}}\).

Tương tự ta cũng có: \(\dfrac{{SE}}{{SC}} = \dfrac{{S{A^2}}}{{S{C^2}}} = \dfrac{9}{{13}}\).

\( \Rightarrow \dfrac{{{V_{S.ADE}}}}{{{V_{S.ABC}}}} = \dfrac{{SD}}{{SB}}.\dfrac{{SE}}{{SC}} = \dfrac{{81}}{{130}} \Leftrightarrow {V_{S.ADE}} = \dfrac{{81}}{{130}}{V_{S.ABC}}\)

Lại có:

\(\begin{array}{l}{V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{6}.SA.AB.AC.\sin A \le \dfrac{1}{6}.SA.AB.AC = 1\\ \Rightarrow {V_{S.ADE}} \le \dfrac{{81}}{{130}}\end{array}\)

Vậy thể tích lớn nhất của khối chóp \(S.ADE\) là \(\dfrac{{81}}{{130}}\)

Chọn A.