Câu hỏi
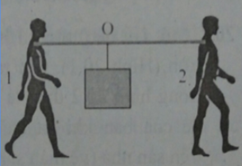
Hai người dùng một cái đòn tre để khiêng một cái hòm (hình vẽ) có trọng lượng 500 N. Khoảng cách giữa hai người là A1A2 = 2 m. Treo hòm vào điểm nào thì lực đè lên vai người một sẽ lớn hớn lực đè lên vai người hai là 100 N. (Bỏ qua trọng lực của đòn).
- A OA1 = 60 cm.
- B OA1 = 70 cm.
- C OA1 = 80 cm.
- D OA1 = 90 cm.
Phương pháp giải:
Quy tắc tổng hợp hai lực song song cùng chiều:
- Hợp lực của hai lực song song cùng chiều là một lực song song, cùng chiều và có độ lớn bằng tổng các độ lớn của hai lực ấy.
- Giá của hợp lực chia khoảng cách giữa hai giá của hai lực song song thành những đoạn tỉ lệ nghịch với độ lớn của hai lực ấy.
\(F = {F_1} + {F_2};\dfrac{{{F_1}}}{{{F_2}}} = \dfrac{{{d_2}}}{{{d_1}}}\) (chia trong)
Lời giải chi tiết:
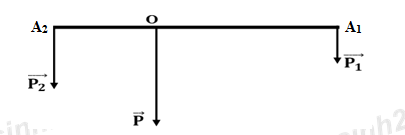
Lực đè lên vai người 1: \(\overrightarrow {{P_1}} \)
Lực đè lên vai người 2: \(\overrightarrow {{P_2}} \)
Theo bài ra ta có: \(\left\{ \begin{array}{l}{P_1} + {P_2} = 500N\\{P_1} - {P_2} = 100N\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{P_1} = 300N\\{P_2} = 200N\end{array} \right.\)
Ta có : \(\dfrac{{{P_2}}}{{{P_1}}} = \dfrac{{O{A_1}}}{{O{A_2}}} = \dfrac{2}{3} \Rightarrow 3O{A_1} = 2O{A_2}\,\,\,\left( 1 \right)\)
Lại có : \(O{A_1} + O{A_2}\; = 2m\,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow \left\{ \begin{array}{l}O{A_1} = 0,8m\\O{A_2} = 1,2m\end{array} \right.\)
Chọn C.







