Câu hỏi
Tam giác \(ABC\) vuông tại \(B\) có \(AB = 3a\), \(BC = a\). Khi quay hình tam giác đó xung quanh đường thẳng \(AB\) một góc 360° ta được một khối tròn xoay. Thể tích của khối tròn xoay đó là:
- A \(3\pi {a^3}\)
- B \(\dfrac{{\pi {a^3}}}{2}\)
- C \(\dfrac{{\pi {a^3}}}{3}\)
- D \(\pi {a^3}\)
Phương pháp giải:
- Khi quay một tam giác vuông theo một cạnh góc vuông, ta được một hình nón có chiều cao là cạnh góc vuông đó, bán kính đường tròn đáy là cạnh góc vuông còn lại, đường sinh là cạnh huyền.
- Áp dụng công thức tính thể tích khối nón \(V = \dfrac{1}{3}\pi {r^2}h\)(r là bán kính đáy, h là độ dài đường cao)
Lời giải chi tiết:
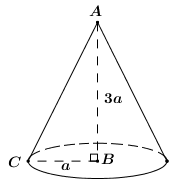
Khi quay tam giác \(ABC\) quanh cạnh \(AB\) ta nhận được một khối nón có chiều cao \(h = AB = 3a\), bán kính đáy \(r = BC = a\).
Vậy thể tích của khối tròn xoay là \(V = \dfrac{1}{3}\pi {a^2}.3a = \pi {a^3}.\)
Chọn D.
Câu hỏi trước
