Phương pháp giải:

Sử dụng công thức giải nhanh: \(R = \dfrac{{{{\left( {canh\,\,ben} \right)}^2}}}{{2h}}\) với \(h\) là chiều cao của hình chóp.

Lời giải chi tiết:

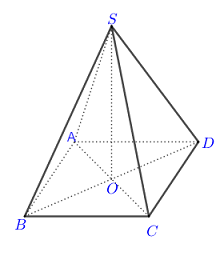
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\).

\(ABCD\) là hình vuông cạnh \(a \Rightarrow AC = a\sqrt 2  \Rightarrow AO = \dfrac{{a\sqrt 2 }}{2}\).

Áp dụng định lí Pytago trong tam giác vuông \(SAO\) có:

\(SO = \sqrt {S{A^2} - A{O^2}}  = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}}  = \dfrac{{a\sqrt 2 }}{2}\).

Vậy \(R = \dfrac{{S{A^2}}}{{2SO}} = \dfrac{{{a^2}}}{{2.\dfrac{{a\sqrt 2 }}{2}}} = \dfrac{{a\sqrt 2 }}{2}.\)

Chọn C.