Câu hỏi
Đồ thị dưới đây là của hàm số nào?
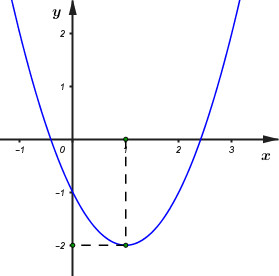
- A \(y = 2{x^2} - 4x - 1.\)
- B \(y = {x^2} - 2x - 1.\)
- C \(y = - {x^2} - 2x + 1.\)
- D \(y = {x^2} + 2x - 1.\)
Phương pháp giải:
Dựa vào đồ thị hàm số, xét dấu của \(a,\,\) suy ra tọa độ đỉnh của parabol và các điểm thuộc đồ thị hàm số để từ đó chọn đáp án đúng.
Lời giải chi tiết:
Gọi hàm số có đồ thị như hình vẽ là \(y = a{x^2} + bx + c\,\,\,\,\left( {a \ne 0} \right).\)
Ta thấy đồ thị hàm số có bề lõm hướng xuống dưới nên \(a > 0 \Rightarrow \) loại đáp án C.
Từ đồ thị hàm số ta thấy đồ thị hàm số có đỉnh là \(I\left( {1; - 2} \right)\) và đi qua điểm \(\left( {0; - 1} \right)\) nên ta có:
\(\left\{ \begin{array}{l}\frac{{ - b}}{{2a}} = 1\\a{.1^2} + b.1 + c = - 2\\a{.0^2} + b.0 + c = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 2a\\c = - 1\\a + b + c = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 2\\c = - 1\end{array} \right. \Rightarrow y = {x^2} - 2x - 1.\)
Chọn B.







