Phương pháp giải:

Lấy lần lượt trên \(SA,\,\,SB,\,\,SC\)các điểm \(M,\,\,N,\,\,P\)sao cho \(SM = SN = SP = 1\). Sử dụng tỉ số thể tích.

Lời giải chi tiết:

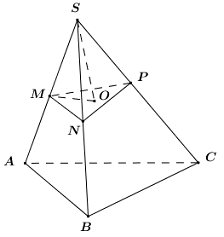
Lấy lần lượt trên \(SA,\,\,SB,\,\,SC\)các điểm \(M,\,\,N,\,\,P\)sao cho \(SM = SN = SP = 1\).

Khi đó các tam giác \(SMN,\,\,SNP,\,\,SMP\) là các tam giác đều cạnh 1.

\( \Rightarrow MN = NP = MP = 1\). Khi đó ta có hình chóp đều \(S.MNP\).

Gọi \(O\)là tâm của tam giác đều \(MNP \Rightarrow SO \bot \left( {MNP} \right)\)và \(MO = \dfrac{2}{3}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{\sqrt 3 }}{3}\).

Ta có \(SO = \sqrt {S{M^2} - M{O^2}}  = \sqrt {1 - {{\left( {\dfrac{{\sqrt 3 }}{3}} \right)}^2}}  = \dfrac{{\sqrt 6 }}{3}.\)

Diện tích tam giác đều \(MNP\) có cạnh bằng 1 là \(S = \dfrac{{\sqrt 3 }}{4}.\)

Khi đó \({V_{S.MNP}} = \dfrac{1}{3}.SO.{S_{MNP}} = \dfrac{1}{3}.\dfrac{{\sqrt 6 }}{3}.\dfrac{{\sqrt 3 }}{4} = \dfrac{{\sqrt 2 }}{{12}}.\)

Mặt khác \(\dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SN}}{{SB}}.\dfrac{{SP}}{{SC}} = \dfrac{1}{2}.\dfrac{1}{3}.\dfrac{1}{7} = \dfrac{1}{{42}}.\)

Vậy \({V_{S.ABC}} = \dfrac{{\sqrt 2 }}{{12}}:\dfrac{1}{{42}} = \dfrac{{7\sqrt 2 }}{2}.\)

Chọn D