Phương pháp giải:

a) Lập bảng giá trị các điểm mà đồ thị hàm số đi qua sau đó vẽ đồ thị các hàm số đã cho.

b) Giải phương trình hoành độ giao điểm của 2 đồ thị hàm số ta tìm được hoành độ giao điểm.

Thế hoành độ giao điểm đó vào một trong hai công thức hàm số của 2 đường thẳng đã cho ta tìm được tung độ của giao điểm. Từ đó ta có tọa độ giao điểm cần tìm

c) Tính OB, AH (H là hình chiếu của A trên OB) để tính diện tích tam giác OAB.

Lời giải chi tiết:

a) Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ.

Ta có bảng giá trị của hai hàm số:

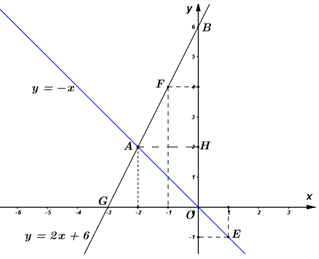
Đồ thị hàm số \(y =  - x\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right);E\left( {1; - 1} \right)\)

Đồ thị hàm số \(y = 2x + 6\) là đường thẳng đi qua hai điểm \(F\left( { - 1;4} \right);\,G\left( { - 3;0} \right)\)

b) Gọi \(A\)  là giao điểm của hai đồ thị nói trên. Tìm tọa độ điểm \(A.\)

Xét phương trình hoành độ giao điểm của hai hàm số: \(y =  - x\) và \(y = 2x + 6\) ta có:

\( - x = 2x + 6\,\,\, \Rightarrow  - 3x = 6\,\,\, \Rightarrow x =  - 2\)

Thay \(x =  - 2\) vào phương trình: \(y =  - x\) ta được \(y = 2\).

Vậy giao điểm \(A\)  của hai đồ thị hàm số có tọa độ là \(A\left( { - 2;2} \right)\).

c) Gọi \(B\)  là giao điểm của đồ thị hàm số \(y = 2x + 6\) với trục tung. Tính diện tích của tam giác \(OAB\)  (với \(O\)  là gốc tọa độ và đơn vị trên các trục tọa độ là xentimet).

Ta có \(B\)  là giao điểm của đồ thị hàm số \(y = 2x + 6\) với trục tung nên \({x_B} = 0 \Rightarrow {y_B} = 2{x_B} + 6 = 6\, \Rightarrow B\left( {0;6} \right)\)

\( \Rightarrow OB = 6\,\,\,\left( {cm} \right)\)

Gọi \(H\)  là hình chiếu của \(A\)  trên \(Oy,\)  khi đó ta sẽ có: \(AH \bot OB = \left\{ H \right\}\) và \(AH = \left| {{x_A}} \right| = 2\,\,\,\left( {cm} \right)\)

Suy ra \({S_{OAB}} = \frac{1}{2}.AH.OB = \frac{1}{2}.2.6 = 6\,\,\,\,\left( {c{m^2}} \right)\)

Vậy diện tích tam giác \(OAB\)  là \(6\,\,c{m^2}\).

Chọn C.