Phương pháp giải:

1) Vẽ đường thẳng trong mặt phẳng Oxy bằng cách xác định hai điểm mà đường thẳng đi qua.

2) Áp dụng định lý Pytago trong tam giác vuông để tính các cạnh của tam giác.

3) Đường thẳng \(y = ax + b\) song song với đường thẳng \(y = a'x + b' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\)

Lời giải chi tiết:

Cho đường thẳng \(\left( d \right):y = 2x - 4\).

1) Xác định tọa độ các giao điểm A, B của \(\left( d \right)\) với hai trục Ox, Oy. Vẽ \(\left( d \right)\) trong mặt phẳng tọa độ Oxy.

+) Giao điểm \(A\)  của đường thẳng \(\left( d \right)\) với trục  \(Ox\)  là: \({y_A} = 0 \Rightarrow 2{x_A} - 4 = 0\, \Rightarrow {x_A} = 2\, \Rightarrow A\left( {2;0} \right)\)

+) Giao điểm  \(B\) của đường thẳng \(\left( d \right)\) với trục  \(Oy\)  là: \({x_B} = 0 \Rightarrow {y_B} = 2{x_B} - 4 =  - 4\, \Rightarrow B\left( {0; - 4} \right)\)

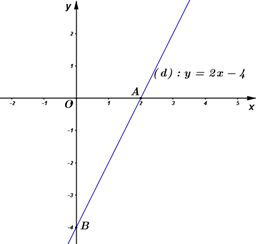
+) Vẽ đường thẳng \(\left( d \right)\) trong mặt phẳng \(Oxy:\)

Ta có đường thẳng \(\left( d \right)\) đi qua hai điểm \(A\left( {2;0} \right);B\left( {0; - 4} \right)\) nên đường thẳng \(\left( d \right)\) chính là đường thẳng \(AB.\)

Ta có hình vẽ:

2) Tính chu vi và diện tích tam giác \(OAB\).

Từ hình vẽ ta thấy \(\Delta OAB\) vuông tại \(O,\,\,OA = 2,\,\,OB = 4\) (đvđd)

Áp dụng định lý Pitago cho tam giác \(OAB\) vuông tại \(O\) ta có:

\(AB = \sqrt {O{A^2} + O{B^2}}  = \sqrt {{2^2} + {4^2}}  = \sqrt {20}  = 2\sqrt 5 \,\) (đvđd)

Chu vi \(\Delta OAB\) là: \({C_{AOB}} = OA + OB + AB = 2 + 4 + 2\sqrt 5  = 6 + 2\sqrt 5 \,\)(đvđd)

Diện tích \(\Delta OAB\):\({S_{OAB}} = \frac{1}{2}.OA.OB = \frac{1}{2}.2.4 = 4\) (đvdt)

Vậy chu vi và diện tích tam giác \(OAB\) lần lượt là \(6 + 2\sqrt 5 \) (đvđd) và \(4\)(đvdt).

3) Tìm \(m\) để đường thẳng \(\left( {{d_m}} \right):y = \left( {{m^2} - 2} \right)x + 2m - 2{m^2}\) song song với  \(\left( d \right)\).

Để đường thẳng \(\left( {{d_m}} \right):y = \left( {{m^2} - 2} \right)x + 2m - 2{m^2}\) song song với \(\left( d \right)\) thì:

\(\begin{array}{l}\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{m^2} - 2 = 2\\2m - 2{m^2} \ne  - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} = 4\\2{m^2} - 2m - 4 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} = 4\\{m^2} - m - 2 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 2\\m =  - 2\end{array} \right.\\\left( {m - 2} \right)\left( {m + 1} \right) \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 2\\m =  - 2\end{array} \right.\\m \ne 2\\m \ne  - 1\end{array} \right. \Leftrightarrow m =  - 2\end{array}\)

Vậy \(m =  - 2\) thì thỏa mãn yêu cầu.