Phương pháp giải:

Dùng phương pháp tọa độ.

Lời giải chi tiết:

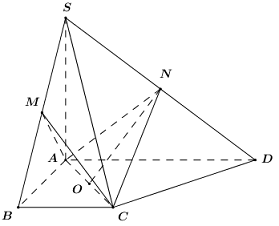
Gọi \(E\) là trung điểm của \(AD\), dễ dàng chứng minh được \(ABCE\) là hình vuông.

\( \Rightarrow CE = a = \dfrac{1}{2}AD \Rightarrow \Delta ACD\) vuông tại \(C\) (tam giác có trung tuyến ứng với 1 cạnh bằng nửa cạnh ấy)

\( \Rightarrow AC \bot CD\). Lại có \(CD \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right) \Rightarrow CD \bot \left( {SAC} \right) \Rightarrow CD \bot SC\).

\( \Rightarrow \Delta SCD\) vuông tại \(C \Rightarrow CN = \dfrac{1}{2}SD\).

Tam giác \(SAD\) vuông tại \(A \Rightarrow AN = \dfrac{1}{2}SD\).

\( \Rightarrow AN = CN \Rightarrow \Delta ANC\) cân tại \(N\).

Gọi \(O\) là trung điểm của \(AC \Rightarrow NO \bot AC\).

Ta có: \(\left\{ \begin{array}{l}\left( {MAC} \right) \bot \left( {NAC} \right)\\\left( {MAC} \right) \cap \left( {NAC} \right) = AC\\\left( {NAC} \right) \supset NO \bot AC\end{array} \right. \Rightarrow NO \bot \left( {MAC} \right) \Rightarrow NO \bot MO\).

Đặt \(SA = x\) ta có: \(SB = \sqrt {{x^2} + {a^2}}  \Rightarrow AM = \dfrac{1}{2}SB = \dfrac{{\sqrt {{x^2} + {a^2}} }}{2}\).

Xét tam giác vuông \(BCM\) có:

\(MC = \sqrt {B{M^2} + B{C^2}}  = \sqrt {\dfrac{{S{B^2}}}{4} + B{C^2}}  = \sqrt {\dfrac{{{x^2} + {a^2}}}{4} + {a^2}}  = \dfrac{{\sqrt {{x^2} + 5{a^2}} }}{2}\) (Định lí Pytago).

Xét tam giác vuông \(ABC\)có: \(AC = \sqrt {A{B^2} + B{C^2}}  = a\sqrt 2 \) (Định lí Pytago) \( \Rightarrow AO = \dfrac{{a\sqrt 2 }}{2}\).

Xét tam giác \(MAC\) có:

\(\begin{array}{l}M{O^2} = \dfrac{{A{M^2} + M{C^2}}}{2} - \dfrac{{A{C^2}}}{4} = \dfrac{{\dfrac{{{x^2} + {a^2}}}{4} + \dfrac{{{x^2} + 5{a^2}}}{4}}}{2} - \dfrac{{2{a^2}}}{4}\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{2{x^2} + 6{a^2}}}{8} - \dfrac{{2{a^2}}}{4} = \dfrac{{{x^2} + 3{a^2}}}{4} - \dfrac{{2{a^2}}}{4} = \dfrac{{{x^2} + {a^2}}}{4}\\ \Rightarrow MO = \dfrac{{\sqrt {{x^2} + {a^2}} }}{2}\end{array}\)

Xét tam giác vuông \(ABD\) có: \(BD = \sqrt {A{B^2} + A{D^2}}  = a\sqrt 5 \).

\(MN\) là đường trung bình của tam giác \(SBD \Rightarrow MN = \dfrac{{a\sqrt 5 }}{2}\).

Xét tam giác vuông \(SAD\) có: \(SD = \sqrt {S{A^2} + A{D^2}}  = \sqrt {{x^2} + 4{a^2}}  \Rightarrow AN = \dfrac{{\sqrt {{x^2} + 4{a^2}} }}{2}\).

Xét tam giác vuông \(OAN\) có: \(ON = \sqrt {A{N^2} - A{O^2}}  = \sqrt {\dfrac{{{x^2} + 4{a^2}}}{4} - \dfrac{{2{a^2}}}{4}}  = \dfrac{{\sqrt {{x^2} + 2{a^2}} }}{2}\).

Ta có: \(NO \bot MO\,\,\left( {cmt} \right) \Rightarrow \Delta OMN\) vuông tại \(O\). Áp dụng định lí Pytago ta có:

\(\begin{array}{l}O{M^2} + O{N^2} = M{N^2} \Rightarrow \dfrac{{{x^2} + {a^2}}}{4} + \dfrac{{{x^2} + 2{a^2}}}{4} = \dfrac{{5{a^2}}}{4}\\ \Rightarrow 2{x^2} + 3{a^2} = 5{a^2} \Leftrightarrow 2{x^2} = 2{a^2} \Leftrightarrow x = a\end{array}\)

\( \Rightarrow SA = a\).

\({S_{ABCD}} = \dfrac{1}{2}\left( {AD + BC} \right).AB = \dfrac{1}{2}\left( {2a + a} \right).a = \dfrac{{3{a^2}}}{2}\).

Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}.a.\dfrac{{3{a^2}}}{2} = \dfrac{{{a^3}}}{2}\).

Chọn B