Phương pháp giải:

+) Gọi \(UCLN\left( {a,b} \right) = d \Rightarrow \left\{ \begin{array}{l}a = d.m\\b = d.n\end{array} \right.,\,\,\,UCLN\,\left( {m,n} \right) = 1,\,\,\left( {m,\,\,n \in {\mathbb{N}^*}} \right).\)

+) Áp dụng CT: \(BCNN\left( {a;\,\,b} \right).UCLN\left( {a;\,\,b} \right) = ab \Rightarrow BCNN\left( {a;\,\,b} \right) = ...\)

+) Tìm \(m;\,\,n\) suy ra \(a{;^{}}b\).

Lời giải chi tiết:

Gọi \(UCLN\left( {a,\,\,b} \right) = d \Rightarrow \left\{ \begin{array}{l}a = md\\b = nd\end{array} \right.,\,\,\,\,UCLN\left( {m,\,\,n} \right) = 1,\,\,m,\,\,n \in {\mathbb{N}^*}.\)

Ta có: \(BCNN\left( {a;\,\,b} \right).UCLN\left( {a,\,\,b} \right) = ab \Rightarrow BCNN\left( {a;\,b} \right) = \frac{{ab}}{{UCLN\left( {a,\,\,b} \right)}} = \frac{{md.nd}}{d} = mnd\).

Mặt khác: \(BCNN\left( {a;\,\,b} \right) - UCLN\left( {a,\,\,b} \right) = 35 \Rightarrow mnd - d = 35 \Rightarrow \left( {mn - 1} \right)d = 35\)

\( \Rightarrow mn - 1 \in U\left( {35} \right) = \left\{ {1;5;7;35} \right\} \Rightarrow mn \in \left\{ {2;\,\,6;\,\,8;36} \right\}\)

+) Với \(d = 1 \Rightarrow mn - 1 = 35 \Rightarrow mn = 36\)

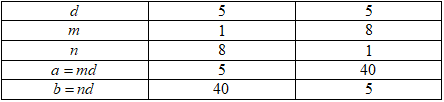
+) Với \(d = 5 \Rightarrow mn - 1 = 7 \Rightarrow mn = 8\)

+) Với \(d = 7 \Rightarrow mn - 1 = 5 \Rightarrow mn = 6\)

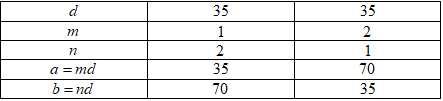
+) Với \(d = 35 \Rightarrow mn - 1 = 1 \Rightarrow mn = 2\)

Vậy ta có các cặp số thỏa mãn bài toán là:

\(\left( {a;\,\,b} \right) = \left\{ {\left( {1;\,36} \right),\,\,\left( {36;\,\,1} \right),\,\,\left( {4;\,\,9} \right),\,\,\left( {9;\,\,4} \right),\,\,\left( {5;\,\,40} \right),\,\,\left( {40;\,\,5} \right),\,\,\left( {7;\,\,42} \right),\,\,\left( {42;\,\,7} \right),\,\,\left( {14;\,\,21} \right),\,\,\left( {21;\,\,14} \right),\,\,\left( {35;\,\,70} \right),\,\,\left( {70;\,\,35} \right)} \right\}.\)

Chọn D.