Câu hỏi
Cho hình chóp \(S.ABC\) có \(SA,SB,SC\) đôi một vuông góc. Biết \(SA = SB = SC = a\), tính thể tích của khối chóp \(S.ABC\).
- A \(\dfrac{{{a^3}}}{6}\).
- B \(\dfrac{{\sqrt 3 {a^3}}}{4}\).
- C \(\dfrac{{{a^3}}}{2}\)
- D \(\dfrac{{{a^3}}}{3}\).
Phương pháp giải:
Thể tích của tứ diện \(OABC\) có \(OA = a,\,\,OB = b,\,\,OC = c\) đôi một vuông góc là: \(V = \dfrac{1}{6}abc.\)
Lời giải chi tiết:
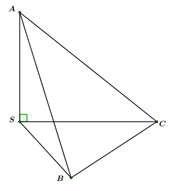
Ta có: \({V_{SABC}} = \dfrac{1}{6}SA.SB.SC = \dfrac{{{a^3}}}{6}.\)
Chọn A.
Câu hỏi trước
