Câu hỏi
Cho hình chóp tam giác \(ABC\) biết \(SA,\,\,SB,\,\,SC\) đôi một vuông góc với nhau và \(SA = a\), \(SB = b\), \(SC = c\). Khi đó bán kính hình cầu ngoại tiếp hình chóp \(S.ABC\)là:
- A \(\sqrt {{a^2} + {b^2} + {c^2}} \)
- B \(\dfrac{{\sqrt {{a^2} + {b^2} + {c^2}} }}{2}\)
- C \(\dfrac{{{a^2} + {b^2} + {c^2}}}{2}\)
- D \({a^2} + {b^2} + {c^2}\)
Lời giải chi tiết:
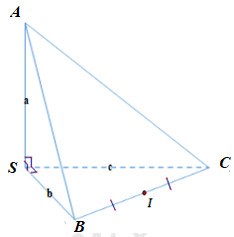
+ Ta có \(SA,\,\,SB,\,\,SC\) đôi một vuông góc \( \Rightarrow SA \bot \left( {SBC} \right)\) và \(\Delta SBC\) vuông tại \(S\).
+ Gọi \(I\) là trung điểm \(BC \Rightarrow I\) tìm đường tròn ngoại tiếp \(\Delta SBC.\)
\( \Rightarrow IC = IB = r = \dfrac{1}{2}BC\)
+ \(\Delta SBC\)vuông tại \(S\)
\( \Rightarrow BC = \sqrt {S{B^2} + S{C^2}} = \sqrt {{b^2} + {c^2}} \Rightarrow r = \dfrac{{\sqrt {{b^2} + {c^2}} }}{2}\).
\( \Rightarrow \)Bán kính mặt cầu ngoại tiếp chóp \(S.ABCD\) là:
\(R = \sqrt {{{\left( {\dfrac{h}{2}} \right)}^2} + {r^2}} = \sqrt {\dfrac{{{a^2}}}{4} + \dfrac{{{b^2} + {c^2}}}{4}} = \dfrac{{\sqrt {{a^2} + {b^2} + {c^2}} }}{2}\).
Chọn B
Câu hỏi trước
