Câu hỏi
Cho hình nón có thiết diện qua trục là một tam giác vuông cân, đường sinh bằng \(a\). Tính diện tích thiết diện qua đỉnh hình nón và tạo với đáy một góc\({60^0}\)
- A \(\dfrac{{{a^2}}}{3}\)
- B \(\dfrac{{{a^2}\sqrt 2 }}{3}\)
- C \({a^2}\sqrt 2 \)
- D \(\dfrac{{{a^2}\sqrt 3 }}{3}\)
Lời giải chi tiết:
+ Thiết diện qua trục là tam giácvuông cân
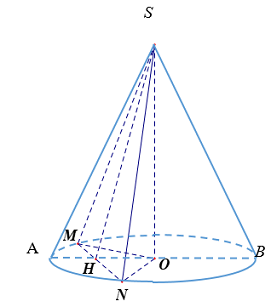
\( \Rightarrow \left\{ \begin{array}{l}SA = SB = a\\AB = a\sqrt 2 \\SO = \dfrac{{AB}}{2} = \dfrac{{a\sqrt 2 }}{2}\\{r_{day}} = OA = \dfrac{{AB}}{2} = \dfrac{{a\sqrt 2 }}{2}\end{array} \right.\)
\( + \) Thiết diện qua đỉnh tạo với đáy \({60^0} \Rightarrow \widehat {SHO} = {60^0}\)
\( + \)\(\tan \widehat {SHO} = \tan {60^0} \Leftrightarrow \dfrac{{SO}}{{OH}} = \sqrt 3 \Leftrightarrow OH = \dfrac{{SO}}{{\sqrt 3 }} = \dfrac{{a\sqrt 6 }}{6}\)
\( + \)\(\sin \widehat {SHO} = \sin {60^0} \Leftrightarrow \dfrac{{SO}}{{SH}} = \dfrac{{\sqrt 3 }}{2} \Leftrightarrow SH = \dfrac{{a\sqrt 6 }}{3}\).
\( + \) Xét \(\Delta OMH\) vuông tại \(H\) có:
\(\begin{array}{l}O{H^2} + M{H^2} = O{M^2} \Leftrightarrow M{H^2} = {\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^2} - {\left( {\dfrac{{a\sqrt 6 }}{6}} \right)^2}\\ \Leftrightarrow MH = \dfrac{{a\sqrt 3 }}{3} \Leftrightarrow MN = 2MH = \dfrac{{2a\sqrt 3 }}{3}\end{array}\)
\( + \)\({S_{\Delta SMN}} = \dfrac{1}{2}.SH.MN = \dfrac{1}{2}.\dfrac{{a\sqrt 6 }}{3}.\dfrac{{2a\sqrt 3 }}{3} = \dfrac{{{a^2}\sqrt 2 }}{3}\).
Chọn B







