Câu hỏi
Cho hình tam giác \(ABC\) vuông tại \(A\) có \(\widehat {ABC} = {30^0}\) và cạnh góc vuông \(AC = 2a\) quay quanh cạnh \(AC\) tạo thành hình nón tròn xoay có diện tích xung quanh bằng:
- A \(\dfrac{4}{3}\pi {a^2}\sqrt 3 \)
- B \(8\pi {a^2}\sqrt 3 \)
- C \(16\pi {a^2}\sqrt 3 \)
- D \(2\pi {a^2}\)
Lời giải chi tiết:
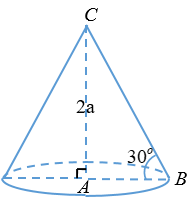
+) Xét \(\Delta ABC\) vuông tại \(A\) có: \(\sin \widehat {ABC} = \dfrac{{AC}}{{BC}}\)
\( \Leftrightarrow \sin \,{30^0}\, = \,\dfrac{{2a}}{{BC}}\, \Rightarrow BC = 4a = l\)
+) \(AB = \sqrt {B{C^2} - A{C^2}} \, = \,\sqrt {{{\left( {4a} \right)}^2} - 4{a^2}} = \,2a\sqrt 3 = r\)
\( \Rightarrow {S_{xq}} = \pi rl = \pi .2a\sqrt 3 .4a = 8\pi {a^2}\sqrt 3 \)
Chọn B
Câu hỏi trước
