Câu hỏi
Cho tam giác \(OAB\) vuông tại \(O\) có \(OA = 3\), \(OB = 4\). Tính diện tích toàn phần của hình nón tạo thành khi quay tam giác \(OAB\) quanh \(OA\).
- A \(S = 36\pi \)
- B \(S = 20\pi \)
- C \(S = 26\pi \)
- D \(S = 52\pi \)
Lời giải chi tiết:
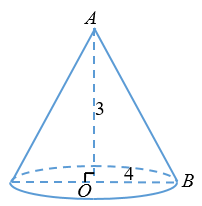
+) \(AB\, = \,l\, = \,\sqrt {O{A^2}\, + \,O{B^2}} = \sqrt {{3^2} + \,\,{4^2}} = 5\)
+)\({S_{xq}}\, = \,\pi rl\, = \,\pi .4.5 = 20\pi \)
\({S_d} = \pi {r^2} = \pi {4^2} = 16\pi \)
\( \Rightarrow {S_{tp}} = {S_{xq}} + \,{S_d} = \,20\pi + 16\pi = 36\pi \)
Chọn A
Câu hỏi trước
