Phương pháp giải:

Công thức tính diện tích xung quanh hình trụ có bán kính đáy \(R,\;\)chiều cao \(h:\;\;{S_{xq}} = 2\pi Rh.\)  

Lời giải chi tiết:

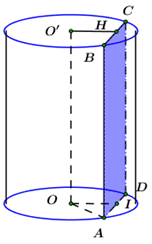
Gọi tâm hai đáy của hình trụ lần lượt là \(O,\,\,O'\) và bán kính đáy là \(R.\)

Theo đề bài ta có, cắt hình trụ bởi mặt phẳng song song với trục nên thiết diện thu được là hình chữ nhật \(ABCD\) (như hình vẽ) với \(AB\) là chiều cao.

Khi đó ta có: \(AB = CD = 5\sqrt 3  \Rightarrow BC = AD = \frac{{30}}{{5\sqrt 3 }} = 2\sqrt 3 .\)

Gọi \(I\) là trung điểm của \(CD \Rightarrow OI = 1.\)

\( \Rightarrow R + \sqrt {O{I^2} + A{I^2}}  = \sqrt {1 + \frac{{{{\left( {2\sqrt 3 } \right)}^2}}}{4}}  = 2.\)

Vậy diện tích xung quanh hình trụ là: \({S_{xq}} = 2\pi Rh = 2\pi .2.5\sqrt 3  = 20\sqrt 3 \pi .\)

Chọn  C.