Phương pháp giải:

Phương trình quỹ đạo: \(y = \left( {\dfrac{g}{{2.v_0^2}}} \right).{x^2}\)

Áp dụng tỉ số lượng giác và định lí Pi – ta – go trong tam giác vuông.

Lời giải chi tiết:

Ta có: \(\left\{ \begin{array}{l}{v_0}\; = 10{\rm{ }}m/s\\g = 10{\rm{ }}m/{s^2}\\\alpha  = {30^0}\end{array} \right.\)

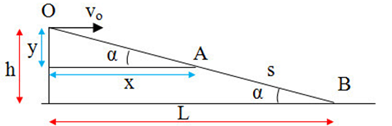
Giả sử vật rơi tại điểm A ở trên dốc có toạ độ (x; y) như hình vẽ:

Phương trình quỹ đạo: \(y = \left( {\dfrac{g}{{2.v_0^2}}} \right).{x^2} = \dfrac{{10}}{{{{2.10}^2}}}.{x^2} \Leftrightarrow y = 0,05{x^2}\,\left( m \right)\,\,\,\,\left( 1 \right)\)

Từ hình vẽ ta có: \(\tan \alpha  = \dfrac{y}{x} \Leftrightarrow \tan 30 = \dfrac{y}{x} \Rightarrow x = \sqrt 3 y\,\,\left( 2 \right)\)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}y = 0,05{x^2}\\x = \sqrt 3 y\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = \dfrac{{20\sqrt 3 }}{3}m\\y = \dfrac{{20}}{3}m\end{array} \right.\)

Khoảng cách từ điểm ném đến điểm rơi: \(OA = \sqrt {{x^2} + {y^2}}  = \sqrt {{{\left( {\dfrac{{20\sqrt 3 }}{3}} \right)}^2} + {{\left( {\dfrac{{20}}{3}} \right)}^2}}  = \dfrac{{40}}{3}m\)

Chọn D.