Câu hỏi
Cho tứ diện đều \(ABCD\) có cạnh bằng 3. Gọi \(M,\,N\) lần lượt là các điểm thuộc các cạnh \(AD,\,BD\) sao cho \(\dfrac{{DM}}{{DA}} = \dfrac{{DN}}{{DB}} = \dfrac{1}{3}.\) Lấy điểm bất kỳ \(P\)trên cạnh \(AB\)(khác \(A,\,B\)). Tính thể tích khối tứ diện \(PMNC.\)
- A \(\dfrac{{3\sqrt 3 }}{2}.\)
- B \(\dfrac{{\sqrt 2 }}{2}.\)
- C \(\dfrac{{7\sqrt 3 }}{2}.\)
- D \(\dfrac{{3\sqrt 7 }}{2}.\)
Lời giải chi tiết:
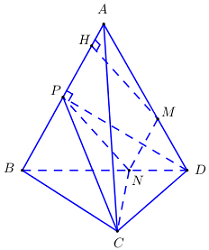
Lấy \(P\) là trung điểm của \(AB\).
\({V_{PMNC}} = {V_{ABCD}} - {V_{P.BCN}} - {V_{MNCD}} - {V_{CAMD}}\).
\(\begin{array}{l} + \,\,{V_{ABCD}} = \dfrac{{27\sqrt 2 }}{{12}}\\ + \,\,{V_{PBCN}} = \dfrac{1}{3}d\left( {P;\left( {BCN} \right)} \right).{S_{BCN}} = \dfrac{1}{3}.\dfrac{1}{2}d\left( {A;\left( {BCN} \right)} \right).\dfrac{2}{3}{S_{BCD}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}.\dfrac{1}{3}d\left( {A;\left( {BCD} \right)} \right).{S_{BCD}} = \dfrac{1}{3}V\\ + \,\,{V_{MNCD}} = \dfrac{1}{3}d\left( {M;\left( {NCD} \right)} \right).{S_{NCD}} = \dfrac{1}{3}.\dfrac{1}{3}d\left( {A;\left( {BCD} \right)} \right).\dfrac{1}{3}{S_{BCD}} = \dfrac{1}{9}V\\ + \,\,{V_{CAMP}} = \dfrac{1}{3}d\left( {C;\left( {AMP} \right)} \right).{S_{AMP}} = \dfrac{1}{3}d\left( {C;\left( {ABD} \right)} \right).\left( {\dfrac{1}{2}MH.AP} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}d\left( {C;\left( {ABD} \right)} \right).\dfrac{1}{2}.\dfrac{2}{3}DP.\dfrac{1}{2}AB = \dfrac{1}{3}BV\\ + \,\,{V_{PMNC}} = \dfrac{2}{9}V = \dfrac{{\sqrt 2 }}{2}\end{array}\)
Chọn B







