Câu hỏi
Cho hình chóp \(S.ABC\) có \(SA\) vuông góc mặt đáy, tam giác \(ABC\) vuông tại \(A\), \(SA = 4\), \(AB = 3\), \(BC = 5\). Tính thể tích khối chóp \(S.ABC\).
- A \(8.\)
- B \(16.\)
- C \(48.\)
- D \(24.\)
Lời giải chi tiết:
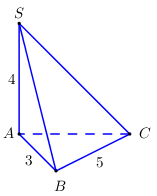
+ \(\Delta ABC\) vuông tại \(A \Rightarrow A{C^2} = B{C^2} - A{B^2} = {5^2} - {3^2} = {4^2} \Rightarrow AC = 4\).
\( \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}.3.4 = 6\).
+ \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{\Delta ABC}} = \dfrac{1}{3}.4.6 = 8\).
Chọn A
Câu hỏi trước
