Lời giải chi tiết:

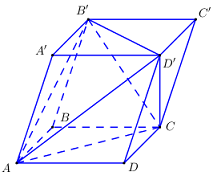
\(\begin{array}{l} + \,\,{V_{CC'B'D'}} = \dfrac{1}{3}h.{S_{\Delta B'C'D'}} = \dfrac{1}{3}h.\dfrac{1}{2}.{S_{A'B'C'D'}}\\ \Leftrightarrow {V_{CC'B'D'}} = \dfrac{1}{6}h.{S_{A'B'C'D'}} = \dfrac{1}{6}V\\ + \,\,{V_{AA'B'D'}} = \dfrac{1}{3}h.{S_{\Delta A'B'D'}} = \dfrac{1}{3}.h.\dfrac{1}{2}.{S_{A'B'C'D'}} = \dfrac{1}{6}.h.{S_{A'B'C'D'}}\\ \Rightarrow {V_{AA'B'D'}} = \dfrac{1}{6}V\\ + \,\,{V_{D'ADC}} = \dfrac{1}{3}.h.{S_{\Delta ADC}} = \dfrac{1}{3}.h.\dfrac{1}{2}.{S_{ABCD}} = \dfrac{1}{6}.h.{S_{ABCD}}\\ \Rightarrow {V_{D'ADC}} = \dfrac{1}{6}V\\ + \,\,{V_{B'ABC}} = \dfrac{1}{3}.h.{S_{\Delta ABC}} = \dfrac{1}{3}.h.\dfrac{1}{2}{S_{ABCD}} = \dfrac{1}{6}.h.{S_{ABCD}}\\ \Rightarrow {V_{B'ABC}} = \dfrac{1}{6}V\end{array}\)

Ta có:

\(\begin{array}{l}{V_{AB'C'D'}} + {V_{CC'B'D'}} + {V_{AA'B'D'}} + {V_{D'ADC}} + {V_{B'ABC}} = {V_{tru}}\\ \Rightarrow {V_{AB'C'D'}} = V - \dfrac{1}{6}.V.4 = \dfrac{1}{3}V\end{array}\)

Chọn A