Câu hỏi
Lăng trụ \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(a\). Hình chiếu vuông góc của \(A'\) lên \(\left( {ABC} \right)\) là trung điểm của \(BC\). Góc giữa cạnh bên và mặt phẳng đáy là \({60^0}\). Khoảng cách từ \(C'\) đến mặt phẳng \(\left( {ABB'A'} \right)\) là:
- A \(\dfrac{{a\sqrt 3 }}{2}\)
- B \(\dfrac{{3a\sqrt {13} }}{{26}}\)
- C \(\dfrac{{3a\sqrt {13} }}{{13}}\)
- D \(\dfrac{{3a\sqrt {10} }}{{20}}\)
Lời giải chi tiết:
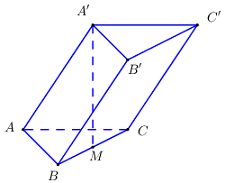
\(A'M = AM.\tan {60^0} = \dfrac{{a\sqrt 3 }}{2}.\sqrt 3 = \dfrac{{3a}}{2}\).
\( \Rightarrow {V_{tru}} = \dfrac{{3a}}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{3{a^3}\sqrt 3 }}{8}\).
\(A'B = \sqrt {A'{M^2} + B{M^2}} = \sqrt {{{\left( {\dfrac{{3a}}{2}} \right)}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt {10} }}{2}\).
\({S_{AA'B}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \dfrac{{{a^2}\sqrt {39} }}{8}\).
\(\left( {AA' = \dfrac{{AM}}{{\cos {{60}^0}}} = a\sqrt 3 } \right)\).
\( \Rightarrow {S_{AA'B'B}} = 2{S_{AA'B}} = \dfrac{{{a^2}\sqrt {39} }}{4}\).
\({V_{tru}} = \dfrac{1}{2}d\left( {C';\left( {AA'B'B} \right)} \right).{S_{AA'B'B}} = \dfrac{{3{a^3}\sqrt 3 }}{8}\).
\( \Rightarrow d\left( {C';\left( {AA'B'B} \right)} \right) = \dfrac{{3a\sqrt {13} }}{{13}}\).
Chọn C







