Câu hỏi
Hình hộp \(ABCD.A'B'C'D'\) có đáy \(A'ABD\) là hình chóp đều, \(AB = a,\,\,AA' = 2a\). Thể tích hình hộp là:
- A \({a^3}\sqrt 3 \)
- B \({a^3}\sqrt 2 \)
- C \({a^3}\dfrac{{\sqrt 2 }}{2}\)
- D \({a^3}\dfrac{{\sqrt {11} }}{2}\)
Lời giải chi tiết:
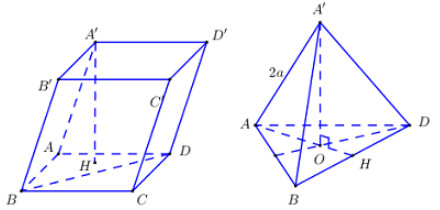
Ta có: \(AO = \dfrac{2}{3}AH = \dfrac{2}{3}\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\).
\( \Rightarrow A'O = \sqrt {AA{'^2} - A{O^2}} = \sqrt {4{a^2} - \dfrac{{{a^2}}}{3}} = \dfrac{{a\sqrt {11} }}{{\sqrt 3 }} = \dfrac{{a\sqrt {33} }}{3}\).
\({S_{ABCD}} = 2{S_{ABD}} = 2\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^2}\sqrt 3 }}{2}\).
\( \Rightarrow {V_{hop}} = A'O.{S_{ABCD}} = \dfrac{{a\sqrt {33} }}{3}.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt {11} }}{2}\).
Chọn D
Câu hỏi trước
