Câu hỏi
Cho hàm số \(y = f\left( x \right)\). Biết \(f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) và hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Hàm số \(g\left( x \right) = f\left( {x - 1} \right)\) đạt cực đại tại điểm nào dưới đây?
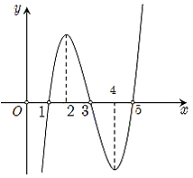
- A \(x = 3.\)
- B \(x = 2.\)
- C \(x = 4\)
- D \(x = 1.\)
Lời giải chi tiết:
\(g\left( x \right) = f\left( {x - 1} \right) \Rightarrow g'\left( x \right) = f'\left( {x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x - 1 = 1\\x - 1 = 3\\x - 1 = 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 4\\x = 6\end{array} \right.\).
\(g'\left( x \right) > 0 \Leftrightarrow f'\left( {x - 1} \right) > 0 \Leftrightarrow \left[ \begin{array}{l}1 < x - 1 < 3\\x - 1 > 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2 < x < 4\\x > 6\end{array} \right.\)
BBT:
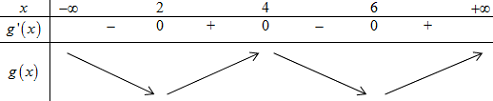
Vậy hàm số đạt cực đại tại \(x = 4\).
Chọn C
Câu hỏi trước
