Câu hỏi
Một hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,\left( {a \ne 0} \right)\) có đồ thị như hình dưới đây. Chọn phát biểu đúng trong các phát biểu dưới đây?
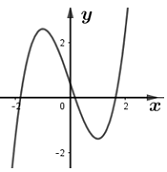
- A \(a > 0,c < 0\)
- B \(a > 0,c > 0\)
- C \(a < 0,b < 0,c < 0\)
- D \(a < 0,c < 0\)
Lời giải chi tiết:
Dựa vào đồ thị hàm số:
+ Nét cuối của đồ thị hàm số hướng lên \( \Rightarrow a > 0\).
+ \(y' = 3a{x^2} + 2bx + c\).
Theo Vi-ét : \({x_1}{x_2} = \dfrac{c}{a}\).
Theo đồ thị hàm số \(\left\{ \begin{array}{l}{x_1} < 0\\{x_2} > 0\end{array} \right. \Rightarrow {x_1}{x_2} < 0 \Leftrightarrow \dfrac{c}{a} < 0\). Mà \(a > 0 \Rightarrow c < 0\).
Chọn A
Câu hỏi trước
