Câu hỏi
Tất cả giá trị của tham số \(m\) để phương trình \({x^3} - 3x - m + 1 = 0\) có ba nghiệm phân biệt, trong đó có hai nghiệm dương là:
- A \( - 1 \le m \le 1\)
- B \( - 1 < m \le 1\)
- C \( - 1 < m < 3\)
- D \( - 1 < m < 1\)
Lời giải chi tiết:
\({x^3} - 3x - m + 1 = 0 \Leftrightarrow {x^3} - 3x + 1 = m\).
Xét \(y = {x^3} - 3x + 1\) ta có \(y' = 3{x^2} - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\).
BBT:
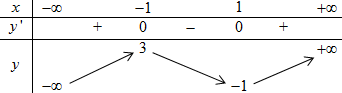
Chọn \(x = 0 \Rightarrow y = 1 \Rightarrow \) Đồ thị hàm số đi qua điểm \(\left( {0;1} \right)\).
Để \({x^3} - 3x - m + 1 = 0\) có 3 nghiệm phân biệt trong đó có 2 nghiệm dương \( \Leftrightarrow - 1 < m < 1\).
Chọn D
Câu hỏi trước
