Lời giải chi tiết:

+ Xét đáp án A: \(y = 2x + \dfrac{2}{{x + 1}} \Rightarrow y' = 2 - \dfrac{2}{{{{\left( {x + 1} \right)}^2}}}\).

  \(y' = 0 \Leftrightarrow {\left( {x + 1} \right)^2} = 1 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  - 2\end{array} \right.\)

   BBT:

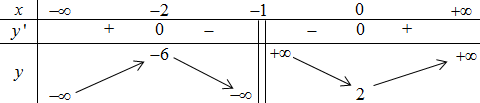
   \( \Rightarrow \) Hàm số có cực trị.

+ Xét đáp án B: \(y = {x^3} + 3{x^2} \Rightarrow y = 3{x^2} + 6x\)

   \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  - 2\end{array} \right.\)

BBT:

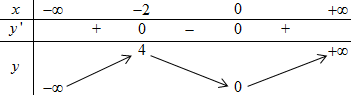
   \( \Rightarrow \) Hàm số có cực trị.

+ Xét đáp án C: \(y =  - {x^4} + 2{x^2} + 3\).

   Vì \(a.b =  - 1.2 =  - 2 < 0 \Rightarrow \) Hàm số có 3 cực trị.

+ Xét đáp án D: \(y = \dfrac{{x + 1}}{{x - 2}} \Rightarrow y' = \dfrac{{ - 3}}{{{{\left( {x - 2} \right)}^2}}} < 0\,\,\forall x \ne 2\).

   \( \Rightarrow \) Hàm số nghịch biến trên \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).

   \( \Rightarrow \) Hàm số không có cực trị.

Chọn D