Lời giải chi tiết:

Gọi phương trình đường thẳng qua \(A\left( {m; - 10} \right)\) có dạng: \(y = k\left( {x - m} \right) - 10\)

Đường thẳng qua A tiếp xúc với đồ thị \( \Rightarrow \left\{ \begin{array}{l}{x^3} - 3{x^2} - 9x + 10 = k\left( {x - m} \right) - 10\,\,\,\left( 1 \right)\\3{x^2} - 6x - 9 = k\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Thế \((2)\) vào \((1)\) ta có:

\(\begin{array}{l}{x^3} - 3{x^2} - 9x + 10 = \left( {3{x^2} - 6x - 9} \right)\left( {x - m} \right) - 10\\ \Leftrightarrow {x^3} - 3{x^2} - 9x + 10 = 3{x^3} - 6{x^2} - 9x - 3m{x^2} + 6mx + 9m - 10\\ \Leftrightarrow 2{x^3} - 3m{x^2} - 3{x^2} + 6mx + 9m - 20 = 0\\ \Leftrightarrow m( - 3{x^2} + 6x + 9) =  - 2{x^3} + 3{x^2} + 20\\ \Leftrightarrow m = \dfrac{{ - 2{x^3} + 3{x^2} + 20}}{{ - 3{x^2} + 6x + 9}}\,\,\,\,\,\left( * \right)\end{array}\)

Để kẻ được đúng 2 tiếp tuyến\( \Rightarrow \) Phương trình (*) phải có 2 nghiệm phân biệt.

Đặt \(f\left( x \right) = \dfrac{{ - 2{x^3} + 3{x^2} + 20}}{{ - 3{x^2} + 6x + 9}}\)

Vẽ bảng biến thiên \(f(x)\) bằng MODE 7

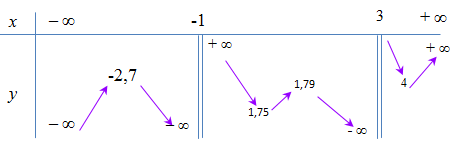
PT (*) có 2 nghiệm phân biệt khi đồ thị \(y = m\) cắt \(f(x)\) tại 2 điểm \( \Rightarrow \left[ \begin{array}{l}m =  - 2,7\\m = 1,75\\m = 1,79\\m = 4\end{array} \right. \Rightarrow S = 4,8\).

Chọn C