Lời giải chi tiết:

Phương trình hoành độ giao điểm:

\( - x + m = \dfrac{x}{{x - 1}} \Leftrightarrow \left( {x - 1} \right)\left( { - x + m} \right) = x \Leftrightarrow  - {x^2} + mx - m = 0\,\,\left( 1 \right)\)

+ Theo đlí viet: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - b}}{a} = m\\{x_1}.{x_2} = \dfrac{c}{a} = m\end{array} \right.\)

+ Để đường thẳng (d) cắt (C) tại 2 điểm phân biệt

\( \Rightarrow \)Phương trình (1) có 2 nghiệm phân biệt khác 1

\( \Rightarrow \left\{ \begin{array}{l}\Delta  > 0\\ - 1 - m - m \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 4m > 0\\m \ne 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < 0\\m > 4\end{array} \right.\)

+ Giả sử phương trình (1) có 2 nghiệm \({x_1},{x_2} \Rightarrow \left\{ \begin{array}{l}A\left( {{x_1}; - {x_1} + m} \right)\\B\left( {{x_2}; - {x_2} + m} \right)\end{array} \right.\)

+ Gọi I là trung điểm AB \( \Rightarrow I\left( {\dfrac{{{x_1} + {x_2}}}{2};\dfrac{{ - \left( {{x_1} + {x_2}} \right) + 2m}}{2}} \right) \Leftrightarrow I\left( {\dfrac{m}{2};\dfrac{m}{2}} \right)\)

+ Vì hai điểm A, B cách đều đường thẳng \(2x - 4y + 5 = 0\)

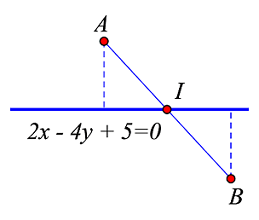
\( \Rightarrow \)Trung điểm I thuộc đường thẳng (như hình vẽ bên).

..Thay I vào đường thẳng ta có: \(2.\dfrac{m}{2} - 4.\dfrac{m}{2} + 5 = 0 \Leftrightarrow m = 5\).

Chọn D